Question

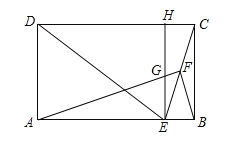
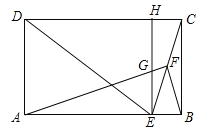
【题目】如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．

（1）求证：DE=DC；

（2）求证：AF⊥BF；

（3）当AFGF=28时，请直接写出CE的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

试题（1）根据平行线的性质以及角平分线的定义，即可得到∠DCE=∠DEC，进而得出DE=DC；

（2）连接DF，根据等腰三角形的性质得出∠DFC=90°，再根据直角三角形斜边上中线的性质得出BF=CF=EF=EC，再根据SAS判定△ABF≌△DCF，即可得出∠AFB=∠DFC=90°，据此可得AF⊥BF；

（3）根据等角的余角相等可得∠BAF=∠FEH，再根据公共角∠EFG=∠AFE，即可判定△EFG∽△AFE，进而得出EF2=AFGF=28，求得EF=，即可得到CE=2EF=．

试题解析：解：（1）∵四边形ABCD是矩形，∴AB∥CD，∴∠DCE=∠CEB，∵EC平分∠DEB，∴∠DEC=∠CEB，∴∠DCE=∠DEC，∴DE=DC；

（2）如图，连接DF，∵DE=DC，F为CE的中点，∴DF⊥EC，∴∠DFC=90°，在矩形ABCD中，AB=DC，∠ABC=90°，∴BF=CF=EF=EC，∴∠ABF=∠CEB，∵∠DCE=∠CEB，∴∠ABF=∠DCF，在△ABF和△DCF中，∵BF=CF，∠ABF=∠DCF，AB=DC，∴△ABF≌△DCF（SAS），∴∠AFB=∠DFC=90°，∴AF⊥BF；

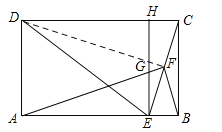
（3）CE=．理由如下：∵AF⊥BF，∴∠BAF+∠ABF=90°，∵EH∥BC，∠ABC=90°，∴∠BEH=90°，∴∠FEH+∠CEB=90°，∵∠ABF=∠CEB，∴∠BAF=∠FEH，∵∠EFG=∠AFE，∴△EFG∽△AFE，∴，即EF2=AFGF，∵AFGF=28，∴EF=，∴CE=2EF=．