题目内容
函数y1=a1x2+b1x+c1,y2=a2x2+b2x+c2满足
=
=
=k;(k≠0,1).则称抛物线y1,y2互为“关联抛物线”,则下列关于“关联抛物线”的说法不正确的是( )
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| A、y1,y2开口方向、开口大小不一定相同 |
| B、若当x=t时y2有最值,那么此时y1也有最值 |
| C、如果y2的最值为m,则y1的最值为km |
| D、如果y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离为|k|d |
考点:二次函数的性质
专题:新定义
分析:由于
=
=
=k,而k≠1,则a1≠a2,于是根据二次项系数的意义对A进行判断;利用比例的性质得-
=-
,根据二次函数的性质得到“关联抛物线”的对称轴相同,于是可对B进行判断;由比例的性质得到a1=kb2,b1=kb2,c1=kc2,再利用顶点的坐标公式对C进行判断;根据抛物线与x轴两交点间的距离公式对D进行判断.
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| b1 |
| 2a1 |
| b2 |
| 2a2 |
解答:解:A、由于
=
=
=k,而k≠1,则a1≠a2,所以y1,y2开口方向不一定相同,开口大小不相同,所以A选项的说法正确;
B、由于
=
=
=k,则
=
,即-
=-
,所以“关联抛物线”的对称轴相同,所以B选项的说法正确;
C、由于
=
=
=k,则a1=kb2,b1=kb2,c1=kc2,y1的最值=
=
=k•
=km,所以C选项的说法正确;
D、由于
=
=
=k,则a1=kb2,b1=kb2,c1=kc2,y1与x轴的两交点间距离=
=
=
=d,所以D选项的说法错误.
故选D.
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
B、由于
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| b1 |
| a1 |
| b2 |
| a2 |
| b1 |
| 2a1 |
| b2 |
| 2a2 |
C、由于
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| 4a1c1-b12 |
| 4a1 |
| 4ka2•kc2-(kb2)2 |
| 4ka2 |
| 4a2c2-b22 |
| 4a2 |
D、由于
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| ||
| |a1| |
| ||
| |ka2| |
| ||
| |a2| |
故选D.
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.也考查了抛物线与x轴两交点间的距离公式.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
方程x2+6x=5的左边配成完全平方后所得方程为( )
| A、(x+3)2=14 |
| B、(x-3)2=14 |
| C、(x+6)2=12 |
| D、以上答案均不对 |

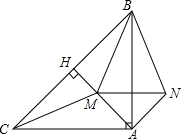 如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.
如图,在△ABC中,∠BAC=90°,AB=AC,AH⊥BC于点H,M为线段AH上一点(与A,H不重合)连CM,BM.