题目内容
如图，AB=10cm，AC=6cm，且D是AC的中点，则BD= cm
考点：两点间的距离
专题：
分析：根据线段中点的性质，可得AD的长，根据线段的和差，可得BD的长．
解答：解：由D是AC的中点，AC=6cm，得
AD=
AC=
×6=3cm．
由线段的和差，得
BD=AB-AD=10-3=7cm，
故答案为：7．
AD=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差，得
BD=AB-AD=10-3=7cm，
故答案为：7．
点评：本题考查了两点间的距离，利用了线段中点的性质，线段的和差．
练习册系列答案
天天练口算系列答案
相关题目
如图所示，在长方形ABCD中，AB=5cm．BC=6cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向终点C以2cm/s的速度移动，两点同时移动，当一动点到达终点时，另一个动点停止移动，连接PQ，设运动时间为t秒．
如图，在△ABC中，点D、E分别在AB、BC上，且DE∥AC，∠BDE=56°，∠C=52°，求∠B的度数．函数y1=a1x2+b1x+c1，y2=a2x2+b2x+c2满足
=
=
=k；（k≠0，1）．则称抛物线y1，y2互为“关联抛物线”，则下列关于“关联抛物线”的说法不正确的是（ ）
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| A、y1，y2开口方向、开口大小不一定相同 |
| B、若当x=t时y2有最值，那么此时y1也有最值 |
| C、如果y2的最值为m，则y1的最值为km |
| D、如果y2与x轴的两交点间距离为d，则y1与x轴的两交点间距离为|k|d |
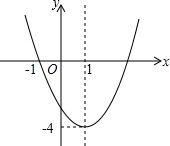已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（ ）| A、二次函数的图象关于直线x=1对称 |
| B、当x＞1时，y随x的增大而减小 |
| C、-1和3是方程ax2+bx+c=0（a≠0）的两个根 |
| D、函数y=ax2+bx+c（a≠0）的最小值是-4 |
如图，把△ABC绕着顶点A逆时针旋转50°，得到△ADE，其中点B的对应点D恰好落在AC边上，点F，G分别是AC，AE上的点，AF=AG，延长BF交DG于点H．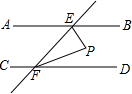
已知，如图AB∥CD，∠AEF与∠EFC的角平分线相交于点P，试说明EP⊥PF．下列图形经过折叠，能围成正方体的是（ ）
A、 |
B、 |
C、 |
D、 |