题目内容
13.四边形ABCD的对角线AC,BD相交于点O,下列条件:①AD=BC,AD∥BC;
②AD∥BC,AO=CO;
③AD∥BC,∠ADC=∠ABC;
④AO=CO,AD=BC中,
能判断四边形ABCD是平行四边形的是( )
| A. | ①②④ | B. | ①③④ | C. | ①②③ | D. | ②③④ |
分析 根据一组对边平行且相等的四边形是平行四边形可得①能判定四边形ABCD是平行四边形;②根据AD∥BC可得∠ADB=∠CBD,∠DAC=∠ACB,可利用AAS判定△ADO≌△CBO,进而可得BO=DO,可根据对角线互相平分的四边形是平行四边形判定四边形ABCD是平行四边形;③根据AD∥BC可得∠ADB=∠CBD,再由∠ADC=∠ABC可得∠ABD=∠CDB,进而可得AB∥CD,根据两组对边分别平行的四边形是平行四边形判定四边形ABCD是平行四边形;④不能证明出BO=DO,因此不能判定四边形ABCD是平行四边形.
解答 解:①AD=BC,AD∥BC能判定四边形ABCD是平行四边形;
②AD∥BC,AO=CO能判定四边形ABCD是平行四边形;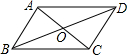
③AD∥BC,∠ADC=∠ABC能判定四边形ABCD是平行四边形;
④AO=CO,AD=BC不能判定四边形ABCD是平行四边形;
故选:C.
点评 此题主要考查了平行四边形的判定,关键是掌握平行四边形的判定定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.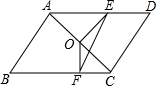 如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )
如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )
 如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )
如图,?ABCD中,O为对角线AC的中点,AC⊥AB,点E为AD中点,并且OF⊥BC,∠D=53°,则∠FOE的度数是( )| A. | 37° | B. | 53° | C. | 127° | D. | 143° |
1.若m>n,下列不等式不一定成立的是( )
| A. | m-2>n-2 | B. | $\frac{m}{2}$>$\frac{n}{2}$ | C. | m2>n2 | D. | 2m+1>2n+1 |
18.地球上水的总储量约为1.39×1018立方米,但目前能被人们生产、生活利用的水只占总储量的0.77%,因此我们要节约用水,那么用科学记数法表示能被人们生产、生活利用的水约为( )
| A. | 1.0703×1015立方米 | B. | 1.0703×1016立方米 | ||
| C. | 1.0703×1017立方米 | D. | 1.0703×1018立方米 |
2.下列计算正确的是( )
| A. | $\sqrt{2}×\sqrt{\frac{1}{2}}=1$ | B. | $\sqrt{{{({-5})}^2}}=-5$ | C. | $\sqrt{6}÷\sqrt{3}=2$ | D. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ |
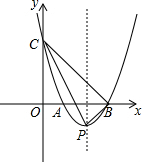 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于点A,B两点,且点B坐标为(3,0). 如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).
如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).