题目内容
15．
已知：如图AE=AC，AD=AB，∠EAC=∠DAB．求证：△EAD≌△CAB．
分析 直接利用全等三角形的判定方法（SAS），进而得出答案．
解答 证明：∵∠EAC=∠DAB，
∴∠EAD=∠CAB，
在△EAD和△CAB中
$\left\{\begin{array}{l}{AE=AC}\\{∠EAD=∠CAB}\\{AD=AB}\end{array}\right.$，
∴△EAD≌△CAB（SAS）．
点评 此题主要考查了全等三角形的判定，正确掌握判定方法是解题关键．
练习册系列答案
53随堂测系列答案
相关题目
5．直线 y=x-1与坐标轴交于A、B两点，点C在x轴上，若△ABC为等腰三角形且S△ABC=$\frac{\sqrt{2}}{2}$，则点C的坐标为（ ）
| A． | 、（0，0 ） | B． | （1-$\sqrt{2}$，0）或（$\sqrt{2}+$1，0） | C． | 、（$\sqrt{2}$+1，0 ） | D． | 、（-$\sqrt{2}$-1，0）或（-$\sqrt{2}$+1，0） |
10．随机抛掷两枚均匀的硬币，落地后至少有一枚正面朝上的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{2}$ |
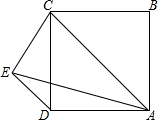在正方形ABCD中，AC为对角线，DE平行于AC，AE=AC，求∠CED的度数．
如图，△ABC中，点E是AB边的中点，点F在AC边上，若以A，E，F为顶点的三角形与△ABC相似，则需要增加的一个条件是∠AFE=∠ABC．（写出一个即可）