题目内容
15.(1)计算:$-{2^2}-|{1-\sqrt{3}}|+2cos30°+201{6^0}$(2)解不等式组:$\left\{\begin{array}{l}{3x>x-2①}\\{\frac{x+1}{3}>2x②}\end{array}\right.$.
分析 (1)直接利用绝对值的性质以及特殊角的三角函数值代入化简求出答案;
(2)分别解不等式进而得出不等式组的解集.
解答 解:(1)$-{2^2}-|{1-\sqrt{3}}|+2cos30°+201{6^0}$
=-4-($\sqrt{3}$-1)+2×$\frac{\sqrt{3}}{2}$+1
=-4-$\sqrt{3}$+1+$\sqrt{3}$+1
=-2;
(2)$\left\{\begin{array}{l}{3x>x-2①}\\{\frac{x+1}{3}>2x②}\end{array}\right.$,
解①得:x>-1,
解②得:x<$\frac{1}{5}$,
故不等式组的解集为:-1<x<$\frac{1}{5}$.
点评 此题主要考查了实数运算以及不等式组的解法,正确化简各数是解题关键.

练习册系列答案
相关题目
3.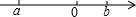 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
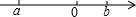 实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )
实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{{a}^{2}}$-$\sqrt{{a}^{2}+2ab+{b}^{2}}$的结果为( )| A. | 2a+b | B. | 2a-b | C. | -2a+b | D. | b |
4.下列命题中逆命题是真命题的是( )
| A. | 对顶角相等 | |
| B. | 若两个角都是45°,那么这两个角相等 | |
| C. | 全等三角形的对应角相等 | |
| D. | 两直线平行,同位角相等 |
5.下列根式中,与$\sqrt{20}$互为同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
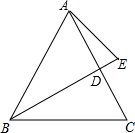 在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.
在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.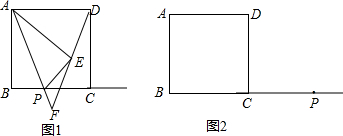
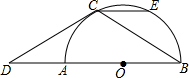 如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.