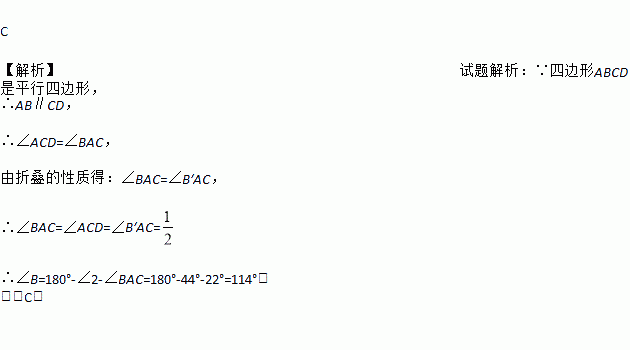题目内容
如图，将?ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（ ）
A. 66° B. 104° C. 114° D. 124°
C
【解析】试题解析：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ACD=∠BAC，
由折叠的性质得：∠BAC=∠B′AC，
∴∠BAC=∠ACD=∠B′AC=
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°；
故选C．
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案如图，在△ABC和△DEC中，∠ABC=∠DEC=90°，连接AD交射线EB于F，AC∥DE，延长CA交射线EB于点G，点F恰好是AD中点。
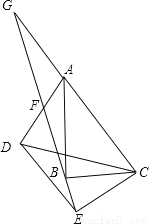
（1）求证：△AFG≌△DFE；
（2）若BC=CE，
①求证：∠ABF=∠DEF；
②若∠BAC=30°，试求∠AFG的度数。
（1）证明见解析（2）①证明见解析②∠AFG=60°。
【解析】试题分析：
（1）由AG∥DE易得：∠G=∠DEF；由F是AD的中点易得AF=DF，结合∠AFG=∠DFE，即可证得：△AGF≌△DEF；
（2）①由BC=CE可得∠CBE=∠CEB，结合∠ABC=DEC=90°，易得∠ABF+∠CBE=90°，∠CEB+∠DEF=90°，从而可得∠ABF=∠DEF；
②由△A... 已知三角形的两边为3和4，则第三边a的取值范围是________．
1＜a＜7
【解析】根据三角形的三边关系：两边之和大于第三边，两边之差小于第三边，得4-3＜a＜4+3，即1＜a＜7．
故答案为：1＜a＜7． 如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．
（1）求证：BE=CD；
（2）连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．
（1）详见解析；（2）.
【解析】试题分析：（1）由平行四边形的性质和角平分线易证∠BAE=∠BEA，根据等腰三角形的性质可得AB=BE；（2）易证△ABE是等边三角形，根据等边三角形的性质可得AE=AB=4，AF=EF=2，由勾股定理求出BF，再由AAS证明△ADF≌△ECF，即△ADF的面积=△ECF的面积，因此平行四边形ABCD的面积=△ABE的面积=AE•BF，即可得出结果．
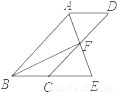
... 如图，在?ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是_______．
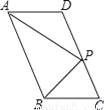
24
【解析】试题分析：∵四边形ABCD是平行四边形，
∴AD∥CB，AB∥CD，
∴∠DAB＋∠CBA＝180°，
又∵AP和BP分别平分∠DAB和∠CBA，
∴∠PAB＋∠PBA＝ (∠DAB＋∠CBA)＝90°，
在△APB中，∠APB＝180°－(∠PAB＋∠PBA)＝90°；
∵AP平分∠DAB，
∴∠DAP＝∠PAB，
∵AB∥CD... 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）
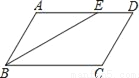
A. 150° B. 130° C. 120° D. 100°
C
【解析】试题分析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABE，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，∵∠BED=150°，∴∠ABE=∠AEB=30°，∴∠A=180°﹣∠ABE﹣∠AEB=120°．故选C． 如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
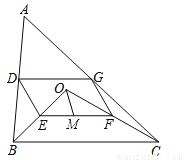
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．
（1）证明见解析；（2）6．
【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；
（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．
试题解析：（1）∵D、G分别是AB、AC的中点，... 如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，若AB＝6，EF＝2，则BC的长为( )
A. 8 B. 10 C. 12 D. 14
B
【解析】试题分析：根据平行四边形的性质可知AB=CD，AD∥BC，AD=BC，然后根据平行线的性质和角平分线的性质可知AB=AF，DE=CD，因此可知AF+DE=AD+EF=2AB=12，解得AD=BC=12-2=10.
故选：B. 直线y=kx+b与抛物线y=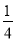
x2交于A（x1，y1）、B（x2，y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为_______________________．
（0，4）
【解析】【解析】
∵直线y=kx+b与抛物线y=x2交于A（x1，y1）、B（x2，y2）两点，∴kx+b=，
化简，得 x2﹣4kx﹣4b=0，∴x1+x2=4k，x1x2=﹣4b．
又∵OA⊥OB，∴ ，
解得，b=4，即直线y=kx+4，故直线恒过顶点（0，4）．
故答案为：（0，4）．