题目内容
7. 在△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE于G.
在△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE于G.求证:(1)CG=EG.
(2)∠B=2∠BCE.
分析 (1)根据HL证明Rt△CDG≌Rt△EDG,进而得出证明结论;
(2)根据等腰三角形的性质解答即可.
解答 证明:(1)∵DE=BE=DC.
在Rt△CDG与Rt△EDG中,
$\left\{\begin{array}{l}{ED=DC}\\{DG=DG}\end{array}\right.$,
∴Rt△CDG≌Rt△EDG(HL).
∴EG=CG.
(2)∵DE=BE.
∴∠B=∠BDE=∠DEC+∠BCE.
∵DE=CD.
∴∠DEC=∠BCE.
∴∠B=2∠BCE.
点评 本题主要考查了全等三角形的判定和性质.解题的关键是判断出三角形EDC为等腰三角形.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 四条边都相等的四边形是菱形 | |
| B. | 有三个角是直角的四边形是矩形 | |
| C. | 对角线互相垂直平分且相等的四边形是正方形 | |
| D. | 一组对边平行,另一组对边相等的四边形是等腰梯形 |
12.下列说法中,正确的是( )
| A. | 延长直线AB | B. | 延长射线OA | ||
| C. | 延长线段AB至C,使AC=BC | D. | 反向延长线段AB至C,使AC=AB |
19.点A、B是数轴上的两个点,若AB=2,点A表示的数是$-\frac{3}{2}$,则点B表示的数是( )
| A. | 2 | B. | -2 | C. | -$\frac{7}{2}$或$\frac{1}{2}$ | D. | 2或-2 |
9.如图所示,函数y=mx+m的图象可能是下列图象中的( )
| A. |  | B. |  | C. |  | D. |  |
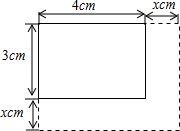 如图,矩形的长是4cm,宽是3cm,如果将其长与宽各增加x cm,那么面积增加y cm2.
如图,矩形的长是4cm,宽是3cm,如果将其长与宽各增加x cm,那么面积增加y cm2.



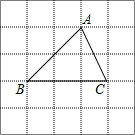 如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形.
如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形.