题目内容
在△ABC中,已知∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB,AC于E、F.
(1)图1中写出等腰三角形,并找出EF与BE、CF间的关系;
(2)图2中∠ABC的平分线与三角形外角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,这时图中还有等腰三角形吗?如果有写出来,此时EF与BE、CF间的关系如何?说明理由.

(1)图1中写出等腰三角形,并找出EF与BE、CF间的关系;
(2)图2中∠ABC的平分线与三角形外角∠ACG的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,这时图中还有等腰三角形吗?如果有写出来,此时EF与BE、CF间的关系如何?说明理由.

考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)由EF∥BC可得∠EOB=∠OBC,由OB平分∠ABC可得∠EBO=∠OBC,由此得到∠EOB=∠EBO,然后即可证明△BEO是等腰三角形,同理可证:△CFO是等腰三角形;根据等腰三角形的性质求得OE=EB,OF=FC,从而证得EF=BE+FC;
(2)根据角平分线的定义以及平行线的性质进行角之间的等量代换,根据等边对等角,发现两个等腰三角形:△BOE和△COF,即可得出所求的结论.
(2)根据角平分线的定义以及平行线的性质进行角之间的等量代换,根据等边对等角,发现两个等腰三角形:△BOE和△COF,即可得出所求的结论.
解答:解:(1)图中的等腰三角形有△BEO和△CFO.
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
同理可证:△CFO是等腰三角形;
(2)EF=BE-CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC;
∴∠ABO=∠EOB,
∴BE=EO;
同理可证:CF=FO;
∵EF=EO-FO,
∴EF=BE-CF.
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
同理可证:△CFO是等腰三角形;
(2)EF=BE-CF.
理由:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵EO∥BC,
∴∠EOB=∠OBC;
∴∠ABO=∠EOB,
∴BE=EO;
同理可证:CF=FO;
∵EF=EO-FO,
∴EF=BE-CF.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,关键灵活运用等腰三角形的性质.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知A、B、C、D依次是直线AD上的4个不同点,则下列说法正确的是( )
| A、线段AD与线段BC是两条相同线段 |
| B、直线AD与直线BC是两条不同直线 |
| C、射线AB于射线AD是两条相同射线 |
| D、射线BC于射线BD是两条里不同射线 |
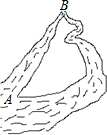 如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )
如图,把原来弯曲的河道改直,A,B两地间的河道长度变短,这样做的道理是( )| A、两点确定一条直线 |
| B、两点确定一条线段 |
| C、两点之间,直线最短 |
| D、两点之间,线段最短 |

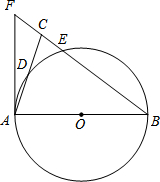 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.