题目内容
6. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①c>0;
②若点B(-$\frac{3}{2}$,y1)、C(-$\frac{5}{2}$,y2)为函数图象上的两点,则y1<y2;
③2a-b=0;
④$\frac{4ac-{b}^{2}}{4a}$<0,
其中,正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据抛物线y轴交点情况可判断;②根据点离对称轴的远近可判断;③根据抛物线对称轴可判断;④根据抛物线与x轴交点个数以及不等式的性质可判断.
解答 解:由抛物线交y轴的正半轴,∴c>0,故①正确;
∵对称轴为直线x=-1,
∴点B(-$\frac{3}{2}$,y1)距离对称轴较近,
∵抛物线开口向下,
∴y1>y2,故②错误;
∵对称轴为直线x=-1,
∴-$\frac{b}{2a}$=-1,即2a-b=0,故③正确;
由函数图象可知抛物线与x轴有2个交点,
∴b2-4ac>0即4ac-b2<0,
∵a<0,
∴$\frac{4ac-{b}^{2}}{4a}$>0,故④错误;
综上,正确的结论是:①③,
故选:B.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c(a≠0),a的符号由抛物线开口方向决定;b的符号由对称轴的位置及a的符号决定;c的符号由抛物线与y轴交点的位置决定;抛物线与x轴的交点个数,决定了b2-4ac的符号.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18.质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
| A. | 点数都是偶数 | B. | 点数的和为奇数 | C. | 点数的和小于13 | D. | 点数的和小于2 |
15.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
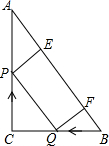 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点P,Q分别从点C,B开始沿边CA,BC匀速运动,点Q的速度为1cm/s,运动时间为ts.过点P作PE⊥AB,过点Q作QF⊥AB,垂足分别为E,F.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点P,Q分别从点C,B开始沿边CA,BC匀速运动,点Q的速度为1cm/s,运动时间为ts.过点P作PE⊥AB,过点Q作QF⊥AB,垂足分别为E,F. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点. 正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$.
正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$. 如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F. 如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.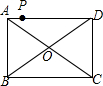 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )