题目内容
12.点P(2m-6,m)到两坐标轴距离相等,则P点坐标为(6,6)或(-2,2).分析 先根据点P到两坐标轴的距离相等列出绝对值方程,然后计算即可.
解答 解:∵点P(2m-6,m)到两坐标轴距离相等,
∴|2m-6|=|m|,
∴2m-6=m或2m-6=-m,
解得m=6或m=2,
∴点P的坐标为(6,6)或(-2,2),
故答案为:(6,6)或(-2,2).
点评 本题考查了点的坐标,列出绝对值方程是解题的关键,难点在于理解互为相反数的两个数的绝对值相等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
7.在Rt△ABC中,∠B=90°,AB=8,BC=6,将△ABC沿MN折叠(M、N分别在AC、AB上,且不与端点重合),使点A与BC上的点D重合,点D把线段BC分成长度之比是1:2的两条线段,则线段BN的长为( )
| A. | $\frac{15}{8}$ | B. | 3 | C. | 3或$\frac{15}{4}$ | D. | $\frac{15}{4}$或4 |
2.下列实数中,属于无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{9}$ | C. | 3.14 | D. | $\frac{1}{3}$ |
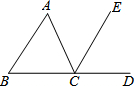 写出图中∠B的一个同位角∠ECD或∠ACD.
写出图中∠B的一个同位角∠ECD或∠ACD.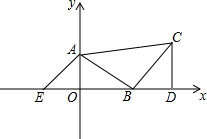 在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.
在直角坐标系中,△ABC是等腰直角三角形,∠ABC=90°,点A(0,3),点B(4,0),CD⊥x轴,垂足为D.