题目内容
13. 如图,在△ABC中,AB=6cm,BC=12cm,AC=9cm,P点以1cm/s的速度从A点出发沿AC方向运动,Q点以2cm/s的速度从C点出发沿CB方向运动,问当P点运动到几秒时,△CPQ与△ABC相似?
如图,在△ABC中,AB=6cm,BC=12cm,AC=9cm,P点以1cm/s的速度从A点出发沿AC方向运动,Q点以2cm/s的速度从C点出发沿CB方向运动,问当P点运动到几秒时,△CPQ与△ABC相似?
分析 设运动时间为ts,则可表示出AP、CQ的长,进一步可表示出CP的长,利用相似三角形的性质可得到关于t的方程,可求得t的值.
解答 解:
设P点运动时间为ts,则AP=t,CQ=2t,
∵AC=9,BC=12,
∴CP=9-t,
若△CPQ与△ABC相似,则有△CPQ∽△CBA和△CPQ∽△CAB两种情况,
①若△CPQ∽△CBA,则$\frac{CP}{CQ}$=$\frac{CB}{CA}$,则有$\frac{9-t}{2t}$=$\frac{12}{9}$,解得t=$\frac{27}{11}$;
②若△CPQ∽△CAB,则$\frac{CP}{CQ}$=$\frac{CA}{CB}$,则有$\frac{9-t}{2t}$=$\frac{9}{12}$,解得t=$\frac{18}{5}$;
综上可知当P点运动到$\frac{27}{11}$秒或$\frac{18}{5}$秒时,△CPQ与△ABC相似.
点评 本题主要考查相似三角形的判定和性质,利用t表示出PC和QC的长,利用相似三角形的性质得到关于t的方程是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
3.一个多边形的内角和大于1100°,小于1400°这个多边形的边数是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.已知x-2y=3,则代数式6-2x+4y的值为( )
| A. | -3 | B. | -1 | C. | 0 | D. | 3 |
1.若x+$\frac{1}{x}$=2,则x2+$\frac{1}{x^2}$=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,将方格纸分成6个三角形,在②③④⑤⑥这5个三角形中,与三角形①相似的三角形有哪些?说明理由!
如图,将方格纸分成6个三角形,在②③④⑤⑥这5个三角形中,与三角形①相似的三角形有哪些?说明理由!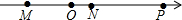 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,那么表示数c的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,那么表示数c的点为( )