Question

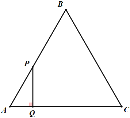
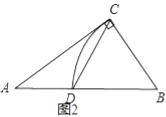
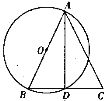
【题目】如图，AB是⊙O的直径，BC交⊙O于点D，E是的中点，连接AE交BC于点F，∠ACB=2∠EAB．

（1）求证：AC是⊙O的切线；

（2）若cosC=，AC=6，求BF的长．

Answer 1

【答案】(1)证明见解析．（2）BF的长为3．

【解析】

（1）证明：连结AD，如图，

∵E是的中点，

∴，

∴∠EAB=∠EAD，

∵∠ACB=2∠EAB，

∴∠ACB=∠DAB，

∵AB是⊙O的直径，

∴∠ADB=90°，

∴∠DAC+∠ACB=90°，

∴∠DAC+∠DAB=90°，即∠BAC=90°，

∴AC⊥AB，

∴AC是⊙O的切线；

（2）解：作FH⊥AB于H，如图，

在Rt△ACD中，∵cosC=，

∴CD=×6=4，

在Rt△ACB中，∵cosC=，

∴BC=×6=9，

∴BD=BC﹣CD=9﹣4=5，

∵∠EAB=∠EAD，即AF平分∠BAD，而FD⊥AD，FH⊥AB，

∴FD=FH，

设BF=x，则DF=FH=5﹣x，

∵FH∥AC，

∴∠HFB=∠C，

在Rt△BFH中，∵cos∠BFH=cosC=，

∴，

解得x=3，即BF的长为3．