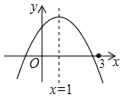
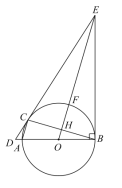
ƒøƒ⁄»›
°æƒø°ø°∞ππ‘ÏÕº–ŒΩ‚°±£¨À¸µƒ”¶”√ Æ∑÷π„∑∫£¨Ãÿ± «”––©ºº«…–‘∫‹«øµƒÃ‚ƒø£¨»Áπ˚≤ªƒ‹∑¢œ÷ƒø÷–À˘“˛∫¨µƒº∏∫Œ“‚“£¨∂¯”√Õ®≥£µƒ¥˙ ˝∑Ω∑®»•Àºøº£¨æ≠≥£»√Œ“√« ÷◊„Œfi¥Î£¨ƒ—“‘œ¬ ÷£¨’‚ ±£¨»Áπ˚ƒ‹◊™ªªÀºŒ¨£¨∑¢œ÷ƒø÷–“˛∫¨µƒº∏∫ŒÃıº˛£¨Õ®π˝ππ‘Ï ∫œµƒº∏∫ŒÕº–Œ£¨Ω´ª·µ√µΩ ¬∞Îπ¶±∂µƒ–ßπ˚£¨œ¬√ÊΩÈ…‹¡Ω‘Ú µ¿˝£∫
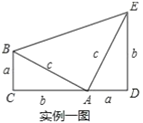
µ¿˝“ª£∫1876ƒÍ£¨√¿π˙◊‹Õ≥Ÿ§∑«∂˚µ¬¿˚”√ µ¿˝“ªÕº÷§√˜¡Àπ¥π…∂®¿Ì£∫”…![]() Àƒ±fl–Œ
Àƒ±fl–Œ![]() µ√
µ√![]() £¨ªØºÚµ√£∫
£¨ªØºÚµ√£∫![]() £Æ
£Æ
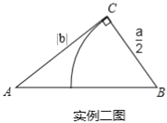
µ¿˝∂˛£∫≈∑º∏¿Ôµ√µƒ°∂º∏∫Œ‘≠±æ°∑º«‘ÿ£¨πÿ”⁄![]() µƒ∑Ω≥Ã
µƒ∑Ω≥Ã![]() µƒÕºΩ‚∑® «£∫ª≠
µƒÕºΩ‚∑® «£∫ª≠![]() £¨ π
£¨ π![]() £¨
£¨![]() £¨
£¨![]() £¨‘Ÿ‘⁄–±±fl
£¨‘Ÿ‘⁄–±±fl![]() …œΩÿ»°
…œΩÿ»°![]() £¨‘Ú
£¨‘Ú![]() µƒ≥§æÕ «∏√∑Ω≥õƒ“ª∏ˆ’˝∏˘(»Á µ¿˝∂˛Õº)£Æ
µƒ≥§æÕ «∏√∑Ω≥õƒ“ª∏ˆ’˝∏˘(»Á µ¿˝∂˛Õº)£Æ
∏˘æ›“‘…œ‘ƒ∂¡≤ƒ¡œªÿ¥œ¬√ʵƒŒ £∫
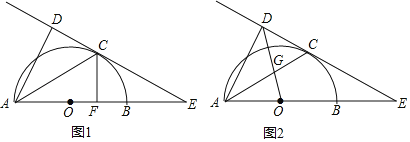
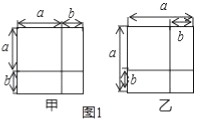
£®1£©»ÁÕº1£¨«Î¿˚”√Õº–Œ÷–√ʪ˝µƒµ»¡øπÿœµ£¨–¥≥ˆº◊Õº“™÷§√˜µƒ ˝—ßπ´ Ω «°°°°°°°°£¨““Õº“™÷§√˜µƒ ˝—ßπ´ Ω «°°°°°°°°£¨ÃÂœ÷µƒ ˝—ßÀºœÎ «°°°°°°°°£ª
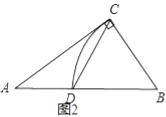
£®2£©»ÁÕº2£¨∞¥’’ µ¿˝∂˛µƒ∑Ω Ωππ‘Ï![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨«Î”√∫¨◊÷ƒ∏
£¨«Î”√∫¨◊÷ƒ∏![]() °¢
°¢![]() µƒ¥˙ ˝ Ω±Ì æ
µƒ¥˙ ˝ Ω±Ì æ![]() µƒ≥§£¨
µƒ≥§£¨![]() µƒ±Ì¥Ô Ωƒ‹∫Õ“——ßµƒ ≤√¥÷™ ∂œ‡¡™œµ£ª
µƒ±Ì¥Ô Ωƒ‹∫Õ“——ßµƒ ≤√¥÷™ ∂œ‡¡™œµ£ª
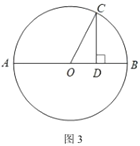
£®3£©»ÁÕº3£¨“—÷™![]() £¨
£¨![]() Œ™÷±æ∂£¨µ„
Œ™÷±æ∂£¨µ„![]() Œ™‘≤…œ“ªµ„£¨π˝µ„
Œ™‘≤…œ“ªµ„£¨π˝µ„![]() ◊˜
◊˜![]() ”⁄µ„
”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨…Ë
£¨…Ë![]() £¨
£¨![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £Æ
£Æ
 °°°°°°°°
°°°°°°°°
 °°°°°°°°
°°°°°°°° °°°°°°°°
°°°°°°°°
°æ¥∞∏°ø£®1£©ÕÍ»´∆Ω∑Ωπ´ Ω£¨∆Ω∑Ω≤Óπ´ Ω£¨ ˝–ŒΩ·∫œµƒÀºœÎ£ª£®2£©![]() £¨
£¨![]() µƒ±Ì¥Ô Ωƒ‹∫Õ“ª‘™∂˛¥Œ∑Ω≥õƒ«Û∏˘π´ Ωœ‡¡™œµ£ª£®3£©÷§√˜º˚Ω‚Œˆ£Æ
µƒ±Ì¥Ô Ωƒ‹∫Õ“ª‘™∂˛¥Œ∑Ω≥õƒ«Û∏˘π´ Ωœ‡¡™œµ£ª£®3£©÷§√˜º˚Ω‚Œˆ£Æ
°æΩ‚Œˆ°ø
£®1£©∏˘æ›¥Û’˝∑Ω–Œ√ʪ˝=∏˜∏ˆ≤ø∑÷√ʪ˝÷Æ∫Õ£¨º¥ø…µ√µΩÕÍ»´∆Ω∑Ωπ´ Ω∫Õ∆Ω∑Ω≤Óπ´ Ω£¨Ω¯∂¯º¥ø…µ√µΩ¥∞∏£ª
£®2£©∏˘æ›π¥π…∂®¿Ì“‘º∞“ª‘™∂˛¥Œ∑Ω≥õƒ«Û∏˘π´ Ω£¨º¥ø…µ√µΩ¥∞∏£ª
£®3£©¡¨Ω”![]() £¨
£¨![]() £¨“◊÷§
£¨“◊÷§![]() £¨
£¨![]() £¨Ω·∫œ
£¨Ω·∫œ![]()
![]() £¨º¥ø…µ√µΩΩ·¬€£Æ
£¨º¥ø…µ√µΩΩ·¬€£Æ
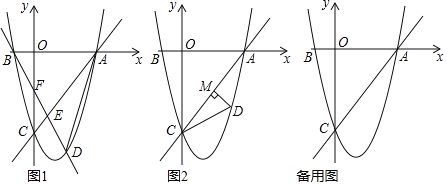
£®1£©»ÁÕº1÷–£¨Õºº◊¥Û’˝∑Ω–Œµƒ√ʪ˝![]() £¨
£¨
Õº““÷–¥Û’˝∑Ω–Œµƒ√ʪ˝![]() £¨º¥£∫
£¨º¥£∫![]() £Æ
£Æ
À¸√«∂ºÃÂœ÷¡À ˝–ŒΩ·∫œµƒÀºœÎ£Æ
π ¥∞∏ «£∫ÕÍ»´∆Ω∑Ωπ´ Ω£¨∆Ω∑Ω≤Óπ´ Ω£¨ ˝–ŒΩ·∫œµƒÀºœÎ£ª
£®2£©°fl‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £ª
£ª
Ω‚![]() £¨”…«Û∏˘π´ Ωø…µ√
£¨”…«Û∏˘π´ Ωø…µ√![]() £¨
£¨
¥£∫![]() µƒ±Ì¥Ô Ωƒ‹∫Õ“ª‘™∂˛¥Œ∑Ω≥õƒ«Û∏˘π´ Ωœ‡¡™œµ£ª
µƒ±Ì¥Ô Ωƒ‹∫Õ“ª‘™∂˛¥Œ∑Ω≥õƒ«Û∏˘π´ Ωœ‡¡™œµ£ª
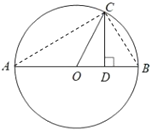
£®3£©”…“—÷™£¨ø…µ√![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() £Æ
£Æ
°fl![]() Œ™÷±æ∂£¨
Œ™÷±æ∂£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°fl![]() £¨
£¨
°‡![]() £¨
£¨![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨
£¨
°‡![]() £¨º¥
£¨º¥![]() £¨
£¨
°fl‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨
°‡![]() £¨º¥
£¨º¥![]() £¨
£¨
°‡![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
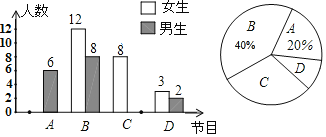
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏°æƒø°ø懿Î÷–øºÃÂøº ±º‰‘Ω¿¥‘ΩΩ¸£¨ƒÍº∂œÎ¡ÀΩ‚≥ı»˝ƒÍº∂1512√˚—ß…˙÷‹ƒ©‘⁄º“Ô˝∂Õ¡∂µƒ«Èøˆ£¨‘⁄≥ı»˝ƒÍº∂Àʪ˙≥È»°¡À18√˚ƒ–…˙∫Õ18√˚≈Æ…˙£¨∂‘À˚√«÷‹ƒ©‘⁄º“µƒ∂Õ¡∂ ±º‰Ω¯––¡Àµ˜≤È£¨≤¢ ’ºØµ√µΩ¡À“‘œ¬ ˝æ›(µ•Œª£∫∑÷÷”)
ƒ–…˙£∫28£¨30£¨32£¨46£¨68£¨39£¨80£¨70£¨66£¨57£¨70£¨95£¨100£¨58£¨69£¨88£¨99£¨105
≈Æ…˙£∫36£¨48£¨78£¨99£¨56£¨62£¨35£¨109£¨29£¨88£¨88£¨69£¨73£¨55£¨90£¨98£¨69£¨72
Õ≥º∆ ˝æ›£¨≤¢÷∆◊˜¡À»Áœ¬Õ≥º∆±Ì£∫
±º‰ |
|
|
|
|
ƒ–…˙ | 2 |
|
| 4 |
≈Æ…˙ | 1 | 5 | 9 | 3 |
∑÷Œˆ ˝æ›£∫¡Ω◊È ˝æ›µƒº´≤Ó°¢∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝»Á±ÌÀ˘ æ
º´≤Ó | ∆Ωæ˘ ˝ | ÷–Œª ˝ | ∑Ω≤Ó | ||
ƒ–…˙ | 77 | 66.7 |
| 70 | 617.3 |
≈Æ…˙ |
| 69.7 | 70.5 |
| 547.2 |
£®1£©«ÎΩ´…œ√ʵƒ±Ì∏Ò≤π≥‰ÕÍ’˚£∫![]() °°°°°°°°£¨
°°°°°°°°£¨![]() °°°°°°°°£¨
°°°°°°°°£¨![]() °°°°°°°°£¨
°°°°°°°°£¨![]() °°°°°°°°£¨
°°°°°°°°£¨![]() °°°°°°°°£ª
°°°°°°°°£ª
£®2£©“—÷™∏√ƒÍº∂ƒ–≈Æ…˙»À ˝≤Ó≤ª∂‡£¨∏˘æ›µ˜≤ȵƒ ˝æ›£¨π¿º∆≥ı»˝ƒÍº∂÷‹ƒ©‘⁄º“∂Õ¡∂µƒ ±º‰‘⁄90∑÷÷”“‘…œ(≤ª∞¸∫¨90∑÷÷”)µƒÕ¨—ß‘º”–∂‡…Ÿ»À£ø
£®3£©Ã”˝¿œ ¶ø¥¡À±Ì∏Ò ˝æ›∫Û»œŒ™≥ı»˝ƒÍº∂µƒ≈Æ…˙÷‹ƒ©∂Õ¡∂◊ˆµ√±»ƒ–…˙∫√£¨«Îƒ„Ω·∫œÕ≥º∆ ˝æ›£¨–¥≥ˆ¡ΩÃı÷ß≥÷Ô˝¿œ ¶π€µ„µƒ¿Ì”…£Æ