题目内容
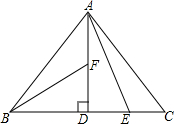 如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数.
如图,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,求∠DBF的度数.考点:全等三角形的判定与性质
专题:
分析:利用等腰三角形的三线合一,直角三角形的性质,可得BD=AD=CD,根据斜边和直角边对应相等可以证明△BDF≌△ADE,利用角的关系即可求得∠DBF的度数.
解答:解:∵AB=AC,AD⊥BC,
∴BD=CD.
又∵∠BAC=90°,
∴BD=AD=CD.
又∵CE=AF,
∴DF=DE.
∴Rt△BDF≌Rt△ADE(SAS).
∴∠DBF=∠DAE=90°-∠AED=90°-62°=28°.
∴BD=CD.
又∵∠BAC=90°,
∴BD=AD=CD.
又∵CE=AF,
∴DF=DE.
∴Rt△BDF≌Rt△ADE(SAS).
∴∠DBF=∠DAE=90°-∠AED=90°-62°=28°.
点评:本题主要考查了全等三角形的判定与性质,解题的关键是熟练运用等腰直角三角形三线合一性质、直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列图形经过折叠,能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
用尺规作图,不能作出唯一三角形的是( )
| A、已知两角和夹边 |
| B、已知两边和其中一边的对角 |
| C、已知两边和夹角 |
| D、已知两角和其中一角的对边 |
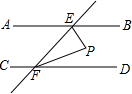 已知,如图AB∥CD,∠AEF与∠EFC的角平分线相交于点P,试说明EP⊥PF.
已知,如图AB∥CD,∠AEF与∠EFC的角平分线相交于点P,试说明EP⊥PF. 如图,边长为a的正六边形内有一边长为a的正三角形,则
如图,边长为a的正六边形内有一边长为a的正三角形,则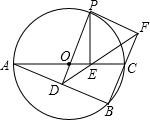 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF. 如图,点M是AB的中点,已知线段BM=5cm,则线段AB的长度为
如图,点M是AB的中点,已知线段BM=5cm,则线段AB的长度为 如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.
如图,已知点A是线段OB的垂直平分线上一点,AN⊥ON,BO⊥ON,P为ON上一点,∠OPB=∠OAB.