题目内容
20.已知x,y,z满足4x-3y-6z=0,x+2y-7z=0,求$\frac{2{x}^{2}+3{y}^{2}+6{z}^{2}}{{x}^{2}+5{y}^{2}+7{z}^{2}}$的值.分析 先解方程组,求得x=3z,y=2z,然后再代入所求代数式进行计算即可.
解答 解:4x-3y-6z=0①,x+2y-7z=0②,
①-②×4得:11y=22z,
解得:y=2z.
将y=2z代入①得:4x-6z-6z=0,
解得:x=3z.
将x=3z,y=2z代入所求代数式得:原式=$\frac{2×(3z)^{2}+3×(2z)^{2}+6{z}^{2}}{(3z)^{2}+5×(2z)^{2}+7{z}^{2}}$=1.
点评 本题主要考查的是求分式的值、解二元一次方程组,求得y=2z、x=3z是解题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
10.甲宿舍有学生8人,乙宿舍有学生3人,要使两个宿舍的人数相等,设从甲宿舍调x人到乙宿舍,则得方程为( )
| A. | 8-x=3-x | B. | 8-x=3+x | C. | 8-x=2(3-x) | D. | 以上都不对 |
5.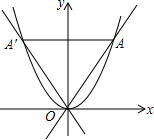 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
 如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )
如图所示,直线y=2x和y=-2x分别与抛物线y=x2交于点O,A和点0,A′,则下列说法中错误的是( )| A. | 点A′和点A关于y轴对称 | |
| B. | △AOA′是等腰三角形 | |
| C. | S△AOA′=8 | |
| D. | 线段OA绕点O逆时针旋转60°可与线段OA′重合 |
 如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识,
如图.已知P为∠ABC平分线上的一点,且PE=PF,结合所学知识, 李明到某影剧城游玩,看见一圆弧形门如图所示,李明想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=40cm,BD=320cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助李明计算出这个圆弧形门的最高点离地面的高度是多少?
李明到某影剧城游玩,看见一圆弧形门如图所示,李明想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=40cm,BD=320cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助李明计算出这个圆弧形门的最高点离地面的高度是多少?