题目内容
10.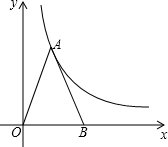 如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )
如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
分析 过A作AC⊥OB于点C,由等腰三角形的性质可求得S△AOC,再由反比例函数k的几何意义可求得k的值.
解答  解:
解:
过A作AC⊥OB于点C,如图,
∵OA=AB,
∴OC=BC=$\frac{1}{2}$OB,
∴S△AOC=$\frac{1}{2}$S△AOB=$\frac{1}{2}$×6=3,
∵双曲线y=$\frac{k}{x}$(k≠0)经过点A,
∴$\frac{1}{2}$|k|=3,且k>0,
∴k=6,
故选C.
点评 本题主要考查反比例函数系数k的几何意义,由条件求得△AOC的面积是解题的关键.

练习册系列答案
相关题目
18.x=1是方程( )的解.
| A. | 1-x=2 | B. | 3-(x-1)=4 | C. | 2x-1=4-3x | D. | x-4=5x-2 |
15. 如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )
如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )
 如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )
如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )| A. | 8$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 32$\sqrt{3}$ | D. | 64$\sqrt{3}$ |
19.与原点距离是2.5个单位长度的点所表示的有理数是( )
| A. | 2.5 | B. | -2.5 | C. | ±2.5 | D. | 这个数无法确定 |
10.设n为正整数,且n<4$\sqrt{6}$<n+1,则n的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |




 如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E.
如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E. 在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC,请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′.
在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC,请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′.