题目内容
5. 如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E.
如图,在△ABC中,三个内角的角平分线交于点O,OE⊥BC于点E.(1)∠ABO+∠BCO+∠CAO=90°;
(2)∠BOD和∠COE的数量关系是∠BOD=∠COE.
分析 (1)直接利用角平分线的性质得出∠ABO=∠CBO,∠DAC=∠BAD,∠BCN=∠ACN,进而利用三角形内角和定理得出答案;
(2)利用三角形外角的性质进而得出答案.
解答 解:(1)∵在△ABC中,三个内角的角平分线交于点O,
∴∠ABO=∠CBO,∠DAC=∠BAD,∠BCN=∠ACN,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ABO+∠BCO+∠CAO=90°;
(2)∠BOD=∠COE,
理由:∵∠BOD=∠ABO+∠BAO,
∠COE=90°-∠OCB,∠ABO+∠BCO+∠CAO=90°,
∴∠BOD=∠COE.
故答案为:∠BOD=∠COE.
点评 此题主要考查了三角形内角和定理以及角平分线的性质,正确掌握角平分线的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.使分式$\frac{{x}^{2}-3}{x+3}$等于0的x值是( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | ±3 | D. | 9 |
13.如表记录了一名球员在罚球线上投篮的结果.
根据这个结果估计,这名球员投篮一次的命中率是0.5(精确到0.1)
| 投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
| 投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
| 投中频率($\frac{m}{n}$) | 0.56 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
14.若△ABC三条边的长度分别为m,n,p.且|m-n|+(m-p)2=0.则这个三角形为( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
 直角梯形有内切圆O(设其半径为R),AC与BD的交点为M,证明:S△BCM=R2.
直角梯形有内切圆O(设其半径为R),AC与BD的交点为M,证明:S△BCM=R2.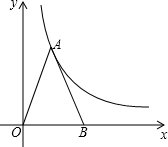 如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )
如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )