题目内容
 有边长为1的等边△ABC和顶角为120°的等腰△DBC,以D为顶点作60°的角,两边分别交于AB、AC于M、N,连结MN,求△AMN的周长?
有边长为1的等边△ABC和顶角为120°的等腰△DBC,以D为顶点作60°的角,两边分别交于AB、AC于M、N,连结MN,求△AMN的周长?考点:全等三角形的判定与性质,角平分线的性质,等边三角形的性质
专题:
分析:要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CND,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.
解答:解:∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°,
∵△ABC是边长为1的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在△BDF和△CND中,
∵
,
∴△BDF≌△CND(SAS),
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠BDM+∠BDF=60°,
在△DMN和△DMF中,
∵
,
∴△DMN≌△DMF(SAS)
∴MN=MF,
∴△AMN的周长是:
AM+AN+MN
=AM+MB+BF+AN
=AB+AC
=1+1
=2.

∴∠BCD=∠DBC=30°,
∵△ABC是边长为1的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在△BDF和△CND中,
∵
|
∴△BDF≌△CND(SAS),
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠BDM+∠BDF=60°,
在△DMN和△DMF中,
∵
|
∴△DMN≌△DMF(SAS)
∴MN=MF,
∴△AMN的周长是:
AM+AN+MN
=AM+MB+BF+AN
=AB+AC
=1+1
=2.
点评:此题考查了全等三角形的判定与性质,等边三角形的性质;主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键,注意:三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
神州七号进入地表上空,绕地球运转一周,一共运转了42100000米,请用科学记数法来表示( )
| A、42.1×106米 |
| B、421×106米 |
| C、0.421×108米 |
| D、4.21×107米 |
 如图,抛物线y=x2-2x-3与直线y=-x+b交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.
如图,抛物线y=x2-2x-3与直线y=-x+b交于A,C两点,与x轴交于点A,B.点P为直线AC下方抛物线上的一个动点(不包括点A和点C),过点P作PN⊥AB交AC与点M,垂足为N,连接AP,CP.设点P的横坐标为m.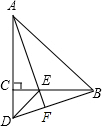 如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD.
如图△ABC和△ECD都是等腰直角三角形,点C在AD上,AE的延长线交BD于点F,求证:AF⊥BD. 已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为
已知二次函数y=x2+2x+m的部分图象如下图所示,则关于x的一元二次方程x2+2x+m=0的解为