题目内容
已知多边形的内角和与外角和的总和为1440°，则这个多边形的边数为（ ）
| A、8 | B、7 | C、6 | D、5 |
考点：多边形内角与外角
专题：
分析：依题意，多边形的内角与外角和为1440°，多边形的外角和为360°，根据内角和公式求出多边形的边数．
解答：解：设多边形的边数为n，根据题意列方程得，
（n-2）•180°+360°=1440°，
n-2=6，
n=8．
故这个多边形的边数为8．
故选：A．
（n-2）•180°+360°=1440°，
n-2=6，
n=8．
故这个多边形的边数为8．
故选：A．
点评：考查了多边形的外角和定理和内角和定理，熟练记忆多边形的内角和公式是解答本题的关键．
练习册系列答案
相关题目
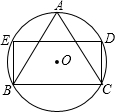如图，△ABC是⊙O的内接等边三角形，AB=1．点D，E在圆上，四边形BCDE为矩形，则这个矩形的面积是（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知a为非负数，比较2a与a的大小关系，正确的是（ ）
| A、2a≥a | B、2a≤a |
| C、2a＜a | D、2a＞a |
已知
=
，那么下列各等式一定成立的是（ ）
| a |
| b |
| c |
| d |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|