题目内容
设a>b>0,a2+b2=4ab,则 的值等于________.
的值等于________.
2
分析:已知等式利用完全平方公式变形,求出a与b的值,代入所求式子计算即可得到结果.
解答:a2+b2=4ab变形得:(a-b)2=2ab,(a+b)2=6ab,
∵0<b<a,
∴a-b>0,a+b>0,
∴a-b= ab,a+b=
ab,a+b= ab,
ab,
∴2a=( +
+ )ab,2b=(
)ab,2b=( -
- )ab,即b=
)ab,即b= =
= ,a=
,a= =
=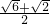 ,
,
则原式= =2
=2 ab=2
ab=2 .
.
故答案为:2 .
.
点评:此题考查了完全平方公式,以及平方差公式,熟练掌握公式是解本题的关键.

分析:已知等式利用完全平方公式变形,求出a与b的值,代入所求式子计算即可得到结果.
解答:a2+b2=4ab变形得:(a-b)2=2ab,(a+b)2=6ab,
∵0<b<a,
∴a-b>0,a+b>0,
∴a-b=
 ab,a+b=
ab,a+b= ab,
ab,∴2a=(
 +
+ )ab,2b=(
)ab,2b=( -
- )ab,即b=
)ab,即b= =
= ,a=
,a= =
=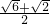 ,
,则原式=
 =2
=2 ab=2
ab=2 .
.故答案为:2
 .
.点评:此题考查了完全平方公式,以及平方差公式,熟练掌握公式是解本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目