题目内容
11.某地区手机收费有两种方式(接听均免费),用户可任选其一:A.月租费0元,拨打电话计费0.18元/分;
B.月租费18元,拨打电话计费0.12元/分.
(1)某用户某月打手机x分钟,请你写出两种方式下该用户应交付的费用(用含x的代数式表示);
(2)若某用户估计一个月内打手机时间为15小时,你认为选用哪种方式更合算?说说你的理由.
分析 (1)应交付费用=月租费+通话费用,把相关数值代入即可求解;
(2)15时=900分,把x=900代入(1)得到的式子,求值后比较即可.
解答 解:(1)∵A.月租费0元,0.18元/分,某月打手机x分钟,
∴A方式应交付费用:0.18x元;
∵月租费18元,0.12元/分,某月打手机x分钟,
∴B方式应交付费用:18+0.12x元;
(2)当x=15时=900分,
A方式用0.18×900=162元;B方式用18+0.12×900=126元,
∵162>126,
所以选用B方式合算.
点评 此题考查列代数式及代数式求值问题,得到两种付费方式的等量关系是解决本题的关键;注意应把时间单位进行统一后再计算.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.若A是一个七次多项式,B也是一个七次多项式,则A+B一定是( )
| A. | 不高于七次多项式或单项式 | B. | 七次多项式 | ||
| C. | 十四次多项式 | D. | 六次多项式 |
16. 有理数 a,b在数轴上的位置如图所示,则a+b的值( )
有理数 a,b在数轴上的位置如图所示,则a+b的值( )
 有理数 a,b在数轴上的位置如图所示,则a+b的值( )
有理数 a,b在数轴上的位置如图所示,则a+b的值( )| A. | 大于0 | B. | 小于0 | C. | 小于 a | D. | 大于 b |
3.4的相反数是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
20.将图1中的正方形剪开得到图2,则图2 中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;…,如此剪下去,则第n个图形中正方形的个数是多少.
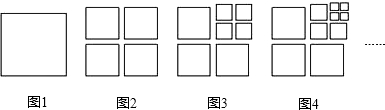
(1)按图示规律填写下表:
(2)按照这种方式剪下去,求第n个图中有多少个正方形;
(3)按照这种方式剪下去,求第200个图中有多少个正方形;
(4)按照这种方式剪下去,求第2017个图中有多少个正方形.

(1)按图示规律填写下表:
| 图 | 1 | 2 | 3 | 4 | 5 | … |
| 正方形个数 | 1 | 4 | 7 | 10 | 13 | … |
(3)按照这种方式剪下去,求第200个图中有多少个正方形;
(4)按照这种方式剪下去,求第2017个图中有多少个正方形.
 在△ABC中,∠C=90°.
在△ABC中,∠C=90°.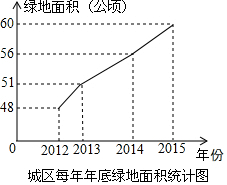 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示). 如图,四边形ABCD是长方形,AC为长方形对角线,画出与△ABC关于AC成轴对称的图形.
如图,四边形ABCD是长方形,AC为长方形对角线,画出与△ABC关于AC成轴对称的图形.