题目内容

如果D，E分别是△ABC的边AB，AC上的点，DE∥BC，
AD
DB
=2，则S△ADE：S△ABC=（　　）
分析：由DE∥BC，即可得△ADE∽△ABC，又由
AD
DB
=2，根据相似三角形的面积比等于相似比的平方，即可求得S△ADE：S△ABC的值．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∵
AD
DB
=2，
∴
AD
AB
=
2
3
，
∴S△ADE：S△ABC=4：9．
故选C．
点评：此题考查了相似三角形的判定与性质．此题难度不大，注意掌握相似三角形面积比等于相似比的平方定理的应用是解此题的关键．
练习册系列答案
相关题目
9、如果a，b分别是2009的两个平方根，那么a+b=
0
．
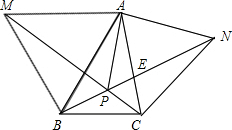如图，AB∥CD．精英家教网
（1）如果∠BAE=∠DCE=45°求∠E的读数．请将下面解的过程补充完整．
因为AB∥CD．
所以∠EAC+45°+∠ACE+45°=
 

所以∠EAC+∠ACE=
 

因为∠EAC+∠ACE+∠E=
 

所以∠E=
 

（2）如果AE、CE分别是∠BAC、∠DCA的平分线，（1）中的结论还成立吗？如果不成立则在下面答不成立；如果成立则答成立，并且说明理由．
答：
 

（3）如果AE、CE分别是∠BAC、∠DCA内部的任意射线，
求证：∠AEC=∠BAE+∠DCE．
精英家教网如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形，MC交BN于P，连PA，则∠APN=
 
．
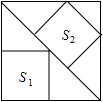如图，大正方形中有2个小正方形，如果它们的面积分别是S1，S2，那么S1，S2的比值是（　　）
（1）如图1，△ABC中，∠ABC与∠ACB的平分线交与点P，求证：∠P=90°+
12
∠A．
（2）如图2，在上题中，如果CP是∠ACD的平分线，BP是∠ABC的平分线，那么∠P与∠A有什么关系？并证明你的结论．
（3）如图3在上题中，如果BP、CP分别是∠CBD与∠BCE的平分线，那么∠P与∠A有什么关系？直接写出关系，不必证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网