Question

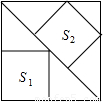
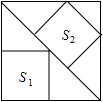如图，大正方形中有2个小正方形，如果它们的面积分别是S₁，S₂，那么S₁，S₂的比值是（　　）

• A．1：1
• B．8：9
• C．9：8
• D．3：2

  2

Answer 1

分析：由四边形ABCD、BEFG、MNQP是正方形，易证得△AEF，△CFG，△APM，△CNQ是等腰直角三角形，即可得AP=PM=PQ=NQ=CQ=

1

3

AC，AE=EF=FG=CG=AF•cos45°=

1

2

AC×

2

2

=

2

4

AC，继而求得S₁与S₂的比值．

解答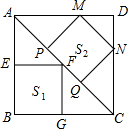：解：∵如图，四边形ABCD、BEFG、MNQP是正方形，
∴∠DAC=∠BAC=∠DCA=∠BCA=45°，∠APM=∠CQN=∠AEF=∠CGF=90°，
∴△AEF，△CFG，△APM，△CNQ是等腰直角三角形，
∴AP=PM=PQ=NQ=CQ=

1

3

AC，AE=EF=FG=CG=AF•cos45°=

1

2

AC×

2

2

=

2

4

AC，
∴S₁=EF²=

1

8

AC²，S₂=PQ²=

1

9

AC²，
∴S₁：S₂=9：8．
故选C．

点评：此题考查了正方形的性质、等腰直角三角形的判定与性质以及特殊角的三角函数值．此题难度适中，注意掌握数形结合思想的应用．