题目内容
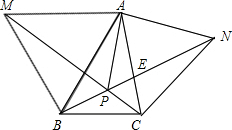 如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形,MC交BN于P,连PA,则∠APN=
如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形,MC交BN于P,连PA,则∠APN=分析:根据等边三角形的三条边相等,每个角都是直角可以证明△ABN与△AMC全等,根据全等三角形对应角相等可以得到∠ANP=∠ACP,然后证明△ANE与△PCE相似,根据相似三角形对应边成比例可得
=
,从而得到△APE与△NCE相似,再根据相似三角形对应角相等的性质即可证明∠APN=∠ACN=60°.
| AE |
| PE |
| NE |
| CE |
解答:解:∵△ABM和△ACN都是等边三角形,
∴AB=AM,AN=AC,∠BAM=∠CAN=60°,
∴∠BAM+∠BAC=∠CAN+∠BAC,
即∠CAM=∠BAN,
在△ABN与△AMC中,
,
∴△ABN≌△AMC(SAS),
∴∠ANP=∠ACP,
又∵∠AEN=∠PEC(对顶角相等),
∴△ANE∽△PCE,
∴
=
,
∵∠AEP=∠NEC(对顶角相等),
∴△APE∽△NCE,
∴∠APN=∠ACN=60°.
故答案为:60°.
∴AB=AM,AN=AC,∠BAM=∠CAN=60°,
∴∠BAM+∠BAC=∠CAN+∠BAC,
即∠CAM=∠BAN,
在△ABN与△AMC中,
|
∴△ABN≌△AMC(SAS),
∴∠ANP=∠ACP,
又∵∠AEN=∠PEC(对顶角相等),
∴△ANE∽△PCE,
∴
| AE |
| PE |
| NE |
| CE |
∵∠AEP=∠NEC(对顶角相等),
∴△APE∽△NCE,
∴∠APN=∠ACN=60°.
故答案为:60°.
点评:本题主要考查了等边三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,判定相似三角形是解题的关键,也是解决本题的难点.

练习册系列答案
相关题目

 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒( ).
).

 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由. 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(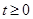 ).
).
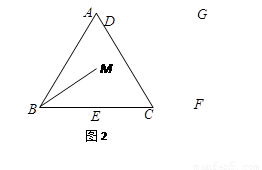
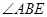 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.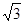 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒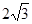 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得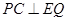 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由 如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形,MC交BN于P,连PA,则∠APN=________.
如果△ABM和△ACN分别是以△ABC的边AB、AC为边的形外等边三角形,MC交BN于P,连PA,则∠APN=________.