题目内容
如图,AB∥CD.
(1)如果∠BAE=∠DCE=45°求∠E的读数.请将下面解的过程补充完整.
因为AB∥CD.
所以∠EAC+45°+∠ACE+45°=
所以∠EAC+∠ACE=
因为∠EAC+∠ACE+∠E=
所以∠E=
(2)如果AE、CE分别是∠BAC、∠DCA的平分线,(1)中的结论还成立吗?如果不成立则在下面答不成立;如果成立则答成立,并且说明理由.
答:
(3)如果AE、CE分别是∠BAC、∠DCA内部的任意射线,
求证:∠AEC=∠BAE+∠DCE.
分析:根据平行线的性质及三角形内角和定理解答.
解答:解:(1)180°(两直线平行,同旁内角互补),90°,180°,90°
(2)∵AE、CE分别是∠BAC、∠DCA的平分线,∴∠EAC+∠ACE=
×180°=90°,故∠E=180°-90°=90°.
(3)∵AE、CE分别是∠BAC、∠DCA内部的任意射线,∴∠BAE+∠EAC+∠DCE+∠ECA=180°,∠AEC+∠CAE+∠ACE=180°,故∠AEC=∠BAE+∠DCE.
(2)∵AE、CE分别是∠BAC、∠DCA的平分线,∴∠EAC+∠ACE=
| 1 |
| 2 |
(3)∵AE、CE分别是∠BAC、∠DCA内部的任意射线,∴∠BAE+∠EAC+∠DCE+∠ECA=180°,∠AEC+∠CAE+∠ACE=180°,故∠AEC=∠BAE+∠DCE.
点评:本题考查的是角平分线、平行线的性质和三角形内角和定理,比较简单.

练习册系列答案
相关题目
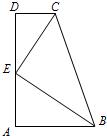 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.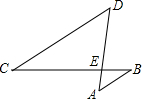 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=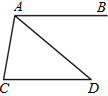 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由. 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )