题目内容
13.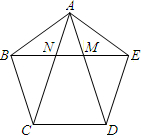 如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N.下列说法:①四边形EDCN是菱形;②正五边形共有5条对角线,它们都想等;③△AEN与△EDM全等.其中说法正确的有①②③(只填序号)
如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N.下列说法:①四边形EDCN是菱形;②正五边形共有5条对角线,它们都想等;③△AEN与△EDM全等.其中说法正确的有①②③(只填序号)
分析 由正五边形的性质可得AB=BC=CD=DE=AE,∠BAE=∠AED=∠CDE=108°,证出BE∥CD,AC∥DE,根据有一组邻边相等的平行四边形是菱形即可证得①正确;由SAS证明△ABE≌△EAD,得出BE=AD,同理:AC=BE=BD=CE,得出②正确;由AAS证明△AEN≌△EDM,得出③正确;即可得出结果.
解答 解:连接BD、CE,如图所示;: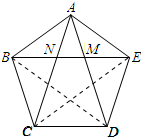
∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,∠BAE=∠AED=∠CDE=108°,
在△ABE和△EAD中,
$\left\{\begin{array}{l}{AB=EA}&{\;}\\{∠BAE=∠AED}&{\;}\\{AD=ED}&{\;}\end{array}\right.$,
∴△ABE≌△EAD(SAS),
∴BE=AD,
同理:AC=BE=BD=CE,
∴AC=BE=BD=CE=AD,②正确;
∵AB=AE,∠BAE=108°,
∴∠AEB=∠ABE=36°,
∴∠DEM=72°,
同理:∠EDM=36°,∠DME=72°,
∴∠DME=72°=∠ANE,
∴∠CDE+∠BED=180°,
∴BE∥CD,
同理:AC∥DE,
∴四边形EDCN是平行四边形,
∵CD=DE,
∴四边形EDCN是菱形,①正确;
在△AEN和△EDM中,
$\left\{\begin{array}{l}{∠AEN=∠EDM}&{\;}\\{∠ANE=∠DME}&{\;}\\{AE=ED}&{\;}\end{array}\right.$,
∴△AEN≌△EDM(SAS);
说法正确的有①②③.
故答案为:①②③.
点评 本题考查了正五边形的性质、全等三角形的判定与性质、平行四边形的判定方法、等腰三角形的性质等知识;本题综合性强,难度适中,熟练掌握正五边形的性质是解决问题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | (2,0) | B. | (0,-2) | C. | (-2,0) | D. | (0,2) |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |