题目内容
4.已知三个有理数a、b、c,其积是负数,其和是正数,当x=$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$时,代数式x2015-2x+2的值为1.分析 根据有理数的运算法则可知a、b、c中有一个负数,从而可知x=1,然后可求得代数式的值.
解答 解:∵三个有理数a、b、c,其积是负数,且和是正数,
∴a、b、c中有一个负数.
∴x=1.
∴原式=12015-2×1+2=1-2+2=1.
故答案为:1.
点评 本题主要考查的是求代数式的值,求得x=1是解题的关键.

练习册系列答案
相关题目
15.下面计算正确的是( )
| A. | -(-3)2=32 | B. | ${(-3)^2}×({\frac{2}{3}})=-6$ | C. | -5-2=-3 | D. | -(-0.2)2=0.22 |
9.点P(2,3)关于原点的对称点的坐标是( )
| A. | (2,3 ) | B. | (-2,-3) | C. | (-2,3) | D. | (-3,2) |
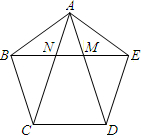 如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N.下列说法:①四边形EDCN是菱形;②正五边形共有5条对角线,它们都想等;③△AEN与△EDM全等.其中说法正确的有①②③(只填序号)
如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N.下列说法:①四边形EDCN是菱形;②正五边形共有5条对角线,它们都想等;③△AEN与△EDM全等.其中说法正确的有①②③(只填序号)