题目内容
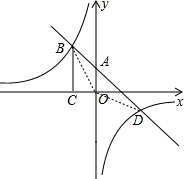
 如图,过y轴上点A的一次函数y=ax+b与反比例函数y=
如图,过y轴上点A的一次函数y=ax+b与反比例函数y=| k |
| x |
(1)求反比例函数和一次函数的解析式;
(2)连结BO、DO,求△BOD的面积;
(3)当x在什么取值范围内,一次函数的值大于反比例函数的值.(直接写出结果)
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把点B的坐标代入反比例函数的解析式求出k即可,然后根据四边形OABC面积求得OA=1,进而求得A的坐标,把A、B的坐标代入y=ax+b即可求得一次函数的解析式;
(2)两个解析式联立,求得点D的坐标,然后根据A、B、D的坐标通过S△BOD=S△AOB+S△AOD即可求得;
(3)利用函数图象求出分别得出使一次函数的值大于反比例函数的值的x的取值范围.
(2)两个解析式联立,求得点D的坐标,然后根据A、B、D的坐标通过S△BOD=S△AOB+S△AOD即可求得;
(3)利用函数图象求出分别得出使一次函数的值大于反比例函数的值的x的取值范围.
解答:解:(1)∵反比例函数y=
的图象经过点B,
∴k=-6,
∴反比例函数解析式为y=-
,
又∵四边形OABC面积为4.
∴(OA+BC)OC=8,
∵BC=3,OC=2,
∴OA=1,
∴A(0,1)
将A、B两点代入y=ax+b有
解得
.
∴一次函数的解析式为y=-x+1,
 ℃
℃
(2)联立组成方程组得
解得x=-2或3,
∴点D(3,-2),
∵B(-2,3),A(0,1),
∴S△BOD=S△AOB+S△AOD=
OA×2+
OA×3=1+
=
,
∴△BOD的面积为
(3)由函数的图象可知当x<-2或0<x<3时一次函数的值大于反比例函数的值.
| k |
| x |
∴k=-6,
∴反比例函数解析式为y=-
| 6 |
| x |
又∵四边形OABC面积为4.
∴(OA+BC)OC=8,
∵BC=3,OC=2,
∴OA=1,
∴A(0,1)
将A、B两点代入y=ax+b有
|
解得
|
∴一次函数的解析式为y=-x+1,
 ℃
℃(2)联立组成方程组得
|
解得x=-2或3,
∴点D(3,-2),
∵B(-2,3),A(0,1),
∴S△BOD=S△AOB+S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
∴△BOD的面积为
| 5 |
| 2 |
(3)由函数的图象可知当x<-2或0<x<3时一次函数的值大于反比例函数的值.
点评:此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式,利用图象判定函数的大小关系是中学的难点同学们应重点掌握.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
下列运算正确的是( )
| A、(-x-y)2=x2+2xy+y2 |
| B、(-a-b) (a+b)=a2-b2 |
| C、(m-3)(m+2)=m2-6 |
| D、(a-b)2=a2-b2 |
 如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.