题目内容
 如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.考点:矩形的性质
专题:
分析:首先连接OP.由矩形ABCD的两边AB=3,BC=4,可求得OA=OD=
,S△AOD=
S矩形ABCD=3,然后由S△AOD=S△AOP+S△DOP=
OA•PE+
OD•PF=
OA(PE+PF)=
×
×(PE+PF)=3,求得答案.
| 5 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答: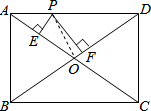 解:连接OP,
解:连接OP,
∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB•BC=12,OA=OC,OB=OD,AC=BD,AC=
=5,
∴S△AOD=
S矩形ABCD=3,OA=OD=
,
∴S△AOD=S△AOP+S△DOP=
OA•PE+
OD•PF=
OA(PE+PF)=
×
×(PE+PF)=3,
∴PE+PF=
.
 解:连接OP,
解:连接OP,∵矩形ABCD的两边AB=3,BC=4,
∴S矩形ABCD=AB•BC=12,OA=OC,OB=OD,AC=BD,AC=
| AB2+BC2 |
∴S△AOD=
| 1 |
| 4 |
| 5 |
| 2 |
∴S△AOD=S△AOP+S△DOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴PE+PF=
| 12 |
| 5 |
点评:此题考查了矩形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,过y轴上点A的一次函数y=ax+b与反比例函数y=
如图,过y轴上点A的一次函数y=ax+b与反比例函数y=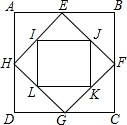 如图,ABCD为60cm×80cm的矩形窗户,内嵌有菱形窗格EFGH和矩形IJKL.矩形窗格IJKL的四个顶点恰好位于菱形窗格EFGH各边的中点.求矩形窗格IJKL的各边长和面积.
如图,ABCD为60cm×80cm的矩形窗户,内嵌有菱形窗格EFGH和矩形IJKL.矩形窗格IJKL的四个顶点恰好位于菱形窗格EFGH各边的中点.求矩形窗格IJKL的各边长和面积.