题目内容
20.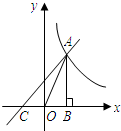 如图,已知一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为( )
如图,已知一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 5 |
分析 可以根据△AOB的面积为1求出k的值,然后联立y=x+1可以求出A的坐标,也可以根据一次函数的解析式求出C的坐标,接着利用勾股定理即可求出AC的长.
解答 解:∵A点是反比例函数y=$\frac{k}{x}$的图象上的点,△AOB的面积为1,
∴$\frac{1}{2}$k=1,
∴k=2,
∴y=$\frac{2}{x}$,
当y=0时,y=x+1=0,
∴x=-1,
∴C的坐标为(-1,0),
而A的坐标满足方程组$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{2}{x}}\end{array}\right.$,
解得x=-2或x=1,
∵A在第一象限,
∴A的横坐标为x=1,纵坐标为y=x+1=2,
∴AC=$\sqrt{(1+1)^{2}+{2}^{2}}$=2$\sqrt{2}$.
故选C.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式和比例函数y=$\frac{k}{x}$中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
13.△ABC的三个外角度数之比是2:3:4,则三个内角度数之比是( )
| A. | 4:3:2 | B. | 3:2:4 | C. | 5:3:1 | D. | 3:1:5 |
8.某元素原子的直径为0.0006纳米(1纳米=10-9米),相当于( )
| A. | 6×10-4米 | B. | 6×10-10米 | C. | 6×10-13米 | D. | 6×10-12米 |
9.据2015年1月24日《桂林日报》报道,临桂县2014年财政收入突破18亿元,在广西各县中排名第二,将18亿用科学记数法表示为( )
| A. | 1.8×10 | B. | 1.8×108 | C. | 1.8×109 | D. | 1.8×1010 |
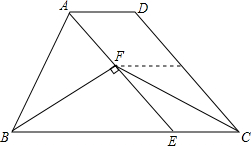 如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.
如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.