题目内容
6.⊙O的半径为5cm,两条弦AB∥CD,AB=8cm、CD=6cm,则两条弦之间的距离为1cm或7cm.分析 此题分为两种情况:两条平行弦在圆心的同侧或两条平行弦在圆心的两侧.根据垂径定理分别求得两条弦的弦心距,进一步求得两条平行弦间的距离.
解答 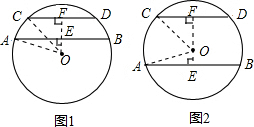 解:如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,则EF⊥CD.
解:如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,则EF⊥CD.
∵OE⊥AB,OF⊥CD,
∴AE=$\frac{1}{2}$AB=4cm,CF=$\frac{1}{2}$CD=3cm.
根据勾股定理,得
OE=$\sqrt{A{O}^{2}-A{E}^{2}}$=3cm;OF=$\sqrt{O{C}^{2}-C{F}^{2}}$=4cm,
①当AB和CD在圆心的同侧时,如图1,则EF=OF-OE=1cm;
②当AB和CD在圆心的两侧时,如图2,则EF=OE+OF=7cm;
则AB与CD间的距离为1cm或7cm.
故答案为1cm或7cm.
点评 本题考查了垂径定理的知识,此题综合运用了垂径定理和勾股定理,特别注意此题要考虑两种情况.

练习册系列答案
相关题目
2.生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件.如果全组共有x名同学,则根据题意列出的方程是( )
| A. | x(x+1)=182 | B. | x(x+1)=182×$\frac{1}{2}$ | C. | x(x-1)=182 | D. | x(x-1)=182×2 |
18. 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )
如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )
 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )
如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则BC的长是( )| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
16.2015年下半年,便民超市某商品的月销量分别是:200,500,350,300,600,350,则这六个数据的中位数是( )
| A. | 600 | B. | 350 | C. | 325 | D. | 300 |
 ∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°.
∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°. 如图,已知∠1+∠2=180°,∠AED=∠C,试判断∠3与∠B的大小关系,在下列解答中填空.
如图,已知∠1+∠2=180°,∠AED=∠C,试判断∠3与∠B的大小关系,在下列解答中填空.