题目内容
3. 如图,△ABC≌△DEF,且△ABC的周长为11,若AB=3,EF=5,则AC=3.
如图,△ABC≌△DEF,且△ABC的周长为11,若AB=3,EF=5,则AC=3.
分析 由全等三角形的性质可求得BC,再由三角形的周长可求得AC.
解答 解:
∵△ABC≌△DEF,
∴BC=EF=5,
∵△ABC的周长为11,若AB=3,
∴AC=11-3-5=3,
故答案为:3.
点评 本题主要考查全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
14.下列等式从左到右的变形中,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x+1=(x+1)2 | C. | x2+2x-1=x(x+2)-1 | D. | x (x-1)=x2-x |
8.已知a+b=4,c-d=3,则(b+c)-(d-a)的值等( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
15.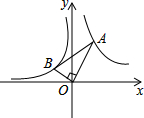 如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
 如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )| A. | $\frac{9}{4}$ | B. | -$\frac{9}{4}$ | C. | -$\frac{3}{4}$ | D. | -3 |
12.下列方程是一元二次方程的是( )
| A. | x-2=0 | B. | x2-4x-1=0 | C. | x3-2x-3=0 | D. | xy+1=0 |
13.已知y=xm-5是y关于x的二次函数,那么m的值为( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 0 |
 如图,在正方形网格图中,若⊙O的半径为2,则阴影部分两个小扇形的面积之和为π.(结果保留π)
如图,在正方形网格图中,若⊙O的半径为2,则阴影部分两个小扇形的面积之和为π.(结果保留π)