题目内容
已知△ABC的三边长a，b，c中b=5，c=3，锐角θ（θ为△ABC的内角）的正弦值是关于x的方程5x2-（a+15）x+3a=0的一个根，试求a的取值范围．
考点：解直角三角形,解一元二次方程-因式分解法
专题：
分析：根据三角形的任意两边之和大于第三边，两边只差小于第三边求出a的取值范围，再解一元二次方程求出θ的正弦值，然后根据锐角的正弦值大于0小于1列出不等式组求出a的取值范围，求a的解集的公共部分即可．
解答：解：∵5-3=2，5+3=8，
∴2＜a＜8，
由因式分解得，（5x-a）（x-3）=0，
所以，5x-a=0，x-3=0，
解得x1=
，x2=3，
∵锐角θ（θ为△ABC的内角）的正弦值是方程的一个解，
∴0＜
＜1，
解得0＜a＜5，
∴a的取值范围是2＜a＜5．
∴2＜a＜8，
由因式分解得，（5x-a）（x-3）=0，
所以，5x-a=0，x-3=0，
解得x1=
| a |
| 5 |
∵锐角θ（θ为△ABC的内角）的正弦值是方程的一个解，
∴0＜
| a |
| 5 |
解得0＜a＜5，
∴a的取值范围是2＜a＜5．
点评：本题考查了解直角三角形，三角形三边关系的应用，关键在于锐角的正弦值大于0小于1．
练习册系列答案
相关题目
如图，矩形ABCD的对角线AC，BD交于点O，EF⊥BD于点O，交AD于点E，交BC于点F，且EF=BF．
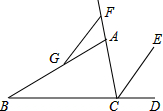如图，CE平分∠ACD，F为CA延长线上一点，FG∥CE交AB于点G，∠ACD=100°，∠AGF=20°，求∠B的度数．
如图，用三个全等的等边三角形纸片，将它们拼成一个与等腰梯形全等的图案，可以怎样拼？在梯形中画出来．
如图，E是△ABC内的一点，AB=AC，连接AE，BE，CE，且BE=CE，延长AE交BC边于点D．求证：AD⊥BC．
把图中的各图补画成以l为对称轴的轴对称图形．