题目内容
9. 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF.(1)求证:四边形ABCD是平行四边形;
(2)图中存在几对相似三角形?分别是什么?请直接写出来不必证明;
(3)求证:OA2=OE•OF.
分析 (1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形;
(2)根据平行相似可以得三角形相似;
(3)由EC∥AB,可得$\frac{OA}{OE}=\frac{OB}{OD}$,由AD∥BC,可得$\frac{OB}{OD}=\frac{OF}{OA}$,等量代换得出$\frac{OA}{OE}=\frac{OF}{OA}$,可得结论.
解答 证明:(1)∵EC∥AB,
∴∠EDA=∠DAB,
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD∥BC,
∵DC∥AB,
∴四边形ABCD为平行四边形;
(2)存在6对三角形相似,分别是:
①∵EC∥AB,
∴△ABF∽△ECF;
②由(1)知:AD∥BC,
∴△EDA∽△ECF;
③∵△ABF∽△ECF,△EDA∽△ECF,
∴△ABF∽△EDA;
④∵四边形ABCD为平行四边形,
∴△ADB∽△CBD;
⑤∵EC∥AB,
∴△OAB∽△OED;
⑥∵AD∥BC,
∴△OBF∽△ODA;
(3)∵EC∥AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}=\frac{OB}{OD}$,
∵AD∥BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}=\frac{OF}{OA}$,
∴$\frac{OA}{OE}=\frac{OF}{OA}$,
∴OA2=OE•OF.
点评 此题考查了相似三角形的判定与性质,平行四边形的判定,平行线的性质,解题时要注意识图,灵活应用数形结合思想.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
20.下列计算正确的是( )
| A. | x2+x4=x6 | B. | x•x2=x3 | C. | x6÷x3=x2 | D. | (-x2y)2=x6y3 |
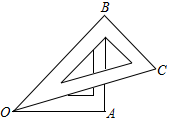 如图,将一副三角板摆放在一起
如图,将一副三角板摆放在一起