题目内容
1.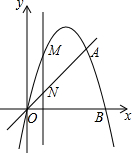 已知抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3)
已知抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3)(1)求b、c、k;
(2)已知直线x=t与抛物线交于点M,与直线y2=kx交于点N
①当点N在OA上时求出线段MN的长a与t的函数关系式,并求出a的最大值;
②以MN为直径作圆,问是否存在这样的t使以MN为直径的圆与y轴相切?如果存在请求出t值,如果不存在请说明理由.
分析 (1)根据题意,抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3),根据待定系数法可求得b、c、k的值.
(2)①由直线x=t与抛物线交于点M,与直线y2=kx交于点N,可以求得点M、N的纵坐标,从而求得线段MN的长a与t的函数关系式,进而求得a的最大值.
②根据①中MN的长a与t的函数关系式和以MN为直径的圆与y轴相切,可以列出关系式,从而求得t的值.
解答 解:(1)∵抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3).
∴3=k×3,$\left\{\begin{array}{l}{0=c}\\{3=-9+3b+c}\end{array}\right.$.
解得k=1,b=4,c=0.
(2)①∵直线x=t与抛物线交于点M,与直线y2=kx交于点N.
∴点M的纵坐标为:-t2+4t,点N的纵坐标为:t.
∴|MN|=-t2+4t-t=-t2+3t.
即a=-t2+3t,(0≤t≤3).
∴$a=-({t-\frac{3}{2})}^{2}+\frac{9}{4}$
∴当t=$\frac{3}{2}$时,a取得最大值$\frac{9}{4}$.
故a与t 的函数关系式为:a=-t2+3t,(0≤t≤3),a的最大值是$\frac{9}{4}$.
②存在.
∵以MN为直径的圆与y轴相切,①中MN的长a与t 的函数关系式为:a=-t2+3t.
∴$\frac{-{t}^{2}+3t}{2}=t$.
解得t1=0,t2=1.
当t=0时,不符合要求,故以MN为直径的圆与y轴相切时,t的值为1.
点评 本题考查二次函数系数的求法,正比例函数k的求值;根据题意列出函数关系式,求最值的问题;探索性问题.关键是可以根据题目中的信息,进行灵活变化求出问题的答案.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案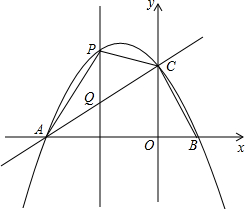 在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x^2}$+bx+c的图象与x轴交于A、B两点,与y轴交于点C,已知A的坐标为(-3,0),tan∠CAB=$\frac{1}{2}$,直线x=m(-1≤m<0)交抛物线于点P,与直线AC交于点Q.
在平面直角坐标系中,抛物线y=-$\frac{1}{2}{x^2}$+bx+c的图象与x轴交于A、B两点,与y轴交于点C,已知A的坐标为(-3,0),tan∠CAB=$\frac{1}{2}$,直线x=m(-1≤m<0)交抛物线于点P,与直线AC交于点Q.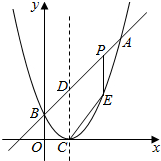 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.