题目内容
10.抛物线y=-x2-2x+3的顶点坐标是(-1,4).分析 已知抛物线的解析式是一般式,用配方法转化为顶点式,根据顶点式的坐标特点,直接写出顶点坐标.
解答 解:∵y=-x2-2x+3=-x2-2x-1+1+3=-(x+1)2+4,
∴抛物线y=-x2-2x+3的顶点坐标是(-1,4).
故答案为:(-1,4).
点评 此题考查了二次函数的性质,二次函数y=a(x-h)2+k的顶点坐标为(h,k),对称轴为x=h,此题还考查了配方法求顶点式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知一次函数y=kx+b(k≠0)的图象是一条直线,这条直线与y轴交于点( )
| A. | (a,0) | B. | (0,a) | C. | (b,0) | D. | (0,b) |
20.五个有理数的积为负数,则五个数中负数的个数是( )
| A. | 5或3 | B. | 3 | C. | 1 | D. | 1或3或5 |
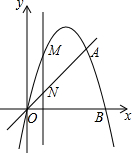 已知抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3)
已知抛物线 y1=-x2+bx+c与直线y2=kx相交于点O(0,0)、点A(3,3) 如图的六边形是正六边形,求∠BAC的大小.
如图的六边形是正六边形,求∠BAC的大小.