ЬтФПФкШн
 ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§y=
ШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§y=| 5 |
| 4 |
ЃЈ1ЃЉЧѓmЕФжЕМАХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШєPЪЧХзЮяЯпЖдГЦжсЩЯвЛЖЏЕуЃЌЁїACPжмГЄзюаЁЪБЃЌЧѓГіPЕФзјБъЃЛ
ЃЈ3ЃЉЪЧЗёДцдкХзЮядкЯпвЛЖЏЕуQЃЌЪЙЕУЁїACQЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуQЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЙ§ЕуPШЮвтзївЛЬѕгыyжсВЛЦНааЕФжБЯпНЛХзЮяЯпгкM1ЃЈx1ЃЌy1ЃЉЃЌM2ЃЈx2ЃЌy2ЃЉСНЕуЃЌЪдЮЪ
| M1P•M2P |
| M1M2 |
ПМЕуЃКЖўДЮКЏЪ§злКЯЬт
зЈЬтЃК
ЗжЮіЃКЃЈ1ЃЉЪзЯШЧѓЕУmЕФжЕЃЌИљОнХзЮяЯпЖдГЦадЕУЕНBЕузјБъЃЌИљОнAЁЂBЕузјБъРћгУНЛЕуЪНЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЃЈ4ЃЉЮЪНЯЮЊИДдгЃЌШчД№ЭМЫљЪОЃЌЗжМИИіВНжшНтОіЃК
Ек1ВНЃКШЗЖЈКЮЪБЁїACPЕФжмГЄзюаЁЃЎРћгУжсЖдГЦЕФаджЪКЭСНЕужЎМфЯпЖЮзюЖЬЕФдРэНтОіЃЛ
Ек2ВНЃКШЗЖЈPЕузјБъPЃЈ1ЃЌ3ЃЉЃЌДгЖјжБЯпM1M2ЕФНтЮіЪНПЩвдБэЪОЮЊy=kx+3-kЃЛ
Ек3ВНЃКРћгУИљгыЯЕЪ§ЙиЯЕЧѓЕУM1ЁЂM2СНЕузјБъМфЕФЙиЯЕЃЌЕУЕНx1+x2=2-4kЃЌx1x2=-4k-3ЃЎетвЛВНЪЧЮЊСЫКѓајЕФИДдгМЦЫузізМБИЃЛ
Ек4ВНЃКРћгУСНЕуМфЕФОрРыЙЋЪНЃЌЗжБ№ЧѓЕУЯпЖЮM1M2ЁЂM1PКЭM2PЕФГЄЖШЃЌЯрЛЅБШНЯМДПЩЕУЕННсТлЃК
=1ЮЊЖЈжЕЃЎетвЛВНЩцМАДѓСПЕФдЫЫуЃЌзЂвтВЛвЊГіДэЃЌЗёдђФбвдЕУГізюКѓЕФНсТлЃЎ
ЃЈ3ЃЉЗжЂйШєCЮЊжБНЧЖЅЕуЃЌЁїACOЯрЫЦгкЁїCQEЃЌЂкШєAЮЊжБНЧЖЅЕуЃЌЁїACOЯрЫЦгкЁїAQEЃЌСНжжЧщПіЬжТлЧѓНтЃЎ
ЃЈ2ЃЉЃЈ4ЃЉЮЪНЯЮЊИДдгЃЌШчД№ЭМЫљЪОЃЌЗжМИИіВНжшНтОіЃК
Ек1ВНЃКШЗЖЈКЮЪБЁїACPЕФжмГЄзюаЁЃЎРћгУжсЖдГЦЕФаджЪКЭСНЕужЎМфЯпЖЮзюЖЬЕФдРэНтОіЃЛ
Ек2ВНЃКШЗЖЈPЕузјБъPЃЈ1ЃЌ3ЃЉЃЌДгЖјжБЯпM1M2ЕФНтЮіЪНПЩвдБэЪОЮЊy=kx+3-kЃЛ
Ек3ВНЃКРћгУИљгыЯЕЪ§ЙиЯЕЧѓЕУM1ЁЂM2СНЕузјБъМфЕФЙиЯЕЃЌЕУЕНx1+x2=2-4kЃЌx1x2=-4k-3ЃЎетвЛВНЪЧЮЊСЫКѓајЕФИДдгМЦЫузізМБИЃЛ
Ек4ВНЃКРћгУСНЕуМфЕФОрРыЙЋЪНЃЌЗжБ№ЧѓЕУЯпЖЮM1M2ЁЂM1PКЭM2PЕФГЄЖШЃЌЯрЛЅБШНЯМДПЩЕУЕННсТлЃК
| M1P•M2P |
| M1M2 |
ЃЈ3ЃЉЗжЂйШєCЮЊжБНЧЖЅЕуЃЌЁїACOЯрЫЦгкЁїCQEЃЌЂкШєAЮЊжБНЧЖЅЕуЃЌЁїACOЯрЫЦгкЁїAQEЃЌСНжжЧщПіЬжТлЧѓНтЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉЁпвЛДЮКЏЪ§y=
x+mОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЃЌ
Ёрm=
ЃЌ
дђCЕФзјБъЮЊЃЈ0ЃЌ
ЃЉЃЌ
 ЁпХзЮяЯпОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ
ЁпХзЮяЯпОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ
ЃЉЃЌЧввджБЯпx=1ЮЊЖдГЦжсЃЌ
дђЕуBЕФзјБъЮЊЃЈ5ЃЌ0ЃЉЃЌ
ЁрЖўДЮКЏЪ§ЮЊy=-
ЃЈx+3ЃЉЃЈx-5ЃЉЛђy=-
x2+
x+
ЃЛ
ЃЈ2ЃЉвЊЪЙЁїACPЕФжмГЄзюаЁЃЌжЛашAP+CPзюаЁМДПЩЃЎ
ШчД№ЭМ2ЃЌСЌНгBCНЛx=1гкPЕуЃЌвђЮЊЕуAЁЂBЙигкx=1ЖдГЦЃЌИљОнжсЖдГЦаджЪвдМАСНЕужЎМфЯпЖЮзюЖЬЃЌПЩжЊДЫЪБAP+CPзюаЁЃЈAP+CPзюаЁжЕЮЊЯпЖЮBCЕФГЄЖШЃЉЃЎ
ЁпBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ
ЃЉЃЌ
ЁржБЯпBCНтЮіЪНЮЊy=-
x+
ЃЌ
ЁпxP=1ЃЌЁрyP=3ЃЌМДPЃЈ1ЃЌ3ЃЉЃЎ
 ЃЈ3ЃЉДцдкЁЃЈ7ЗжЃЉ
ЃЈ3ЃЉДцдкЁЃЈ7ЗжЃЉ
ЩшQЃЈxЃЌ-
x2+
x+
ЃЉ
ЂйШєCЮЊжБНЧЖЅЕуЃЌдђгЩЁїACOЯрЫЦгкЁїCQEЃЌ
ЕУx=5.2ЃЌ
ЂкШєAЮЊжБНЧЖЅЕуЃЌдђгЩЁїACOЯрЫЦгкЁїAQEЃЌ
ЕУx=8.2ЃЌ
ЁрQЕФКсзјБъЮЊ5.2ЃЌ7.2ЃЎ
ЃЈ4ЃЉЪЧЖЈжЕЃЌЖЈжЕЮЊ1ЃЎ
СюОЙ§ЕуPЃЈ1ЃЌ3ЃЉЕФжБЯпЮЊy=kx+bЃЌдђk+b=3ЃЌМДb=3-kЃЌ
дђжБЯпЕФНтЮіЪНЪЧЃКy=kx+3-kЃЌ
Ёпy=kx+3-kЃЌy=-
x2+
x+
ЃЌ
СЊСЂЛЏМђЕУЃКx2+ЃЈ4k-2ЃЉx-4k-3=0ЃЌ
Ёрx1+x2=2-4kЃЌx1x2=-4k-3ЃЎ
Ёпy1=kx1+3-kЃЌy2=kx2+3-kЃЌЁрy1-y2=kЃЈx1-x2ЃЉЃЎ
ИљОнСНЕуМфОрРыЙЋЪНЕУЕНЃК
M1M2=
=
=
ЃЌ
ЁрM1M2=
=
=4ЃЈ1+k2ЃЉЃЎ
гжЁпM1P=
=
=
ЃЛ
ЭЌРэM2P=
ЁрM1P•M2P=ЃЈ1+k2ЃЉ•
=ЃЈ1+k2ЃЉ•
=ЃЈ1+k2ЃЉ•
=4ЃЈ1+k2ЃЉЃЎ
ЁрM1P•M2P=M1M2ЃЌ
Ёр
=1ЮЊЖЈжЕЃЎ
| 5 |
| 4 |
Ёрm=
| 15 |
| 4 |
дђCЕФзјБъЮЊЃЈ0ЃЌ
| 15 |
| 4 |
 ЁпХзЮяЯпОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ
ЁпХзЮяЯпОЙ§ЕуAЃЈ-3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ| 15 |
| 4 |
дђЕуBЕФзјБъЮЊЃЈ5ЃЌ0ЃЉЃЌ
ЁрЖўДЮКЏЪ§ЮЊy=-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
ЃЈ2ЃЉвЊЪЙЁїACPЕФжмГЄзюаЁЃЌжЛашAP+CPзюаЁМДПЩЃЎ
ШчД№ЭМ2ЃЌСЌНгBCНЛx=1гкPЕуЃЌвђЮЊЕуAЁЂBЙигкx=1ЖдГЦЃЌИљОнжсЖдГЦаджЪвдМАСНЕужЎМфЯпЖЮзюЖЬЃЌПЩжЊДЫЪБAP+CPзюаЁЃЈAP+CPзюаЁжЕЮЊЯпЖЮBCЕФГЄЖШЃЉЃЎ
ЁпBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ
| 15 |
| 4 |
ЁржБЯпBCНтЮіЪНЮЊy=-
| 3 |
| 4 |
| 15 |
| 4 |
ЁпxP=1ЃЌЁрyP=3ЃЌМДPЃЈ1ЃЌ3ЃЉЃЎ
 ЃЈ3ЃЉДцдкЁЃЈ7ЗжЃЉ
ЃЈ3ЃЉДцдкЁЃЈ7ЗжЃЉЩшQЃЈxЃЌ-
| 1 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
ЂйШєCЮЊжБНЧЖЅЕуЃЌдђгЩЁїACOЯрЫЦгкЁїCQEЃЌ
ЕУx=5.2ЃЌ
ЂкШєAЮЊжБНЧЖЅЕуЃЌдђгЩЁїACOЯрЫЦгкЁїAQEЃЌ
ЕУx=8.2ЃЌ
ЁрQЕФКсзјБъЮЊ5.2ЃЌ7.2ЃЎ
ЃЈ4ЃЉЪЧЖЈжЕЃЌЖЈжЕЮЊ1ЃЎ
СюОЙ§ЕуPЃЈ1ЃЌ3ЃЉЕФжБЯпЮЊy=kx+bЃЌдђk+b=3ЃЌМДb=3-kЃЌ
дђжБЯпЕФНтЮіЪНЪЧЃКy=kx+3-kЃЌ
Ёпy=kx+3-kЃЌy=-
| 1 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
СЊСЂЛЏМђЕУЃКx2+ЃЈ4k-2ЃЉx-4k-3=0ЃЌ
Ёрx1+x2=2-4kЃЌx1x2=-4k-3ЃЎ
Ёпy1=kx1+3-kЃЌy2=kx2+3-kЃЌЁрy1-y2=kЃЈx1-x2ЃЉЃЎ
ИљОнСНЕуМфОрРыЙЋЪНЕУЕНЃК
M1M2=
| (x1-x2)2+(y1-y2)2 |
| (x1-x2)+k2(x1-x2)2 |
| 1+k2 |
| (x1-x2)2 |
ЁрM1M2=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| (2-4k)2-4(-4k-3) |
гжЁпM1P=
| (x1-1)2+(y1-3)2 |
| (x1-1)2+(kx1+3-k-3)2 |
| 1+k2 |
| (x1-1)2 |
ЭЌРэM2P=
| 1+k2 |
| (x2-1)2 |
ЁрM1P•M2P=ЃЈ1+k2ЃЉ•
| (x1-1)2(x2-1)2 |
| [x1x2-(x1+x2)+1]2 |
| [-4k-3-(2-4k)+1]2 |
ЁрM1P•M2P=M1M2ЃЌ
Ёр
| M1P•M2P |
| M1M2 |
ЕуЦРЃКБОЬтЪЧФбЖШКмДѓЕФжаПМбЙжсЬтЃЌзлКЯПМВщСЫГѕжаЪ§бЇЕФжюЖрживЊжЊЪЖЕуЃКДњЪ§ЗНУцЃЌПМВщСЫЖўДЮКЏЪ§ЕФЯрЙиаджЪЁЂвЛДЮКЏЪ§ЕФЯрЙиаджЪЁЂвЛдЊЖўДЮЗНГЬИљгыЯЕЪ§ЕФЙиЯЕвдМАЖўДЮИљЪНЕФдЫЫуЕШЃЛМИКЮЗНУцЃЌПМВщСЫСНЕуМфЕФОрРыЙЋЪНЁЂжсЖдГЦ-зюЖЬТЗЯпЮЪЬтЕШЃЎБОЬтНтЬтММЧЩвЊЧѓИпЃЌЖјЧвдЫЫуИДдгЃЌвђДЫЖдПМЩњЕФзлКЯФмСІЬсГіСЫКмИпЕФвЊЧѓЃЎ

СЗЯАВсЯЕСаД№АИ
ЯрЙиЬтФП
 ШчЭМЃЌABЪЧЁбOЕФвЛЬѕЯвЃЌODЁЭABДЙзуЮЊCЃЌНЛЁбOгкЕуDЃЌЕуEдкЁбOЩЯЃЎ
ШчЭМЃЌABЪЧЁбOЕФвЛЬѕЯвЃЌODЁЭABДЙзуЮЊCЃЌНЛЁбOгкЕуDЃЌЕуEдкЁбOЩЯЃЎ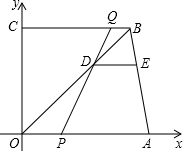 ШчЭМЃЌдкжБНЧЬнаЮOABCжаЃЌOAЁЮBCЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊAЃЈ13ЃЌ0ЃЉЃЌBЃЈ11ЃЌ12ЃЉЃЌЖЏЕуPЃЌQЗжБ№ДгOЁЂBСНЕуЭЌЪБГіЗЂЃЌЕуPвдУПУы2ИіЕЅЮЛЕФЫйЖШбиOAЯђжеЕуAдЫЖЏЃЌЕуQвдУПУы1ИіЕЅЮЛЕФЫйЖШбиBCЯђCдЫЖЏЃЌЕБЕуPЭЃжЙдЫЖЏЪБЃЌЕуQЭЌЪБЭЃжЙдЫЖЏЃЎЯпЖЮOBЁЂPQЯрНЛгкЕуDЃЌЙ§ЕуDзїDEЁЮOAЃЌНЛABгкЕуEЃЌЩшЖЏЕуPЁЂQдЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКsЃЉ
ШчЭМЃЌдкжБНЧЬнаЮOABCжаЃЌOAЁЮBCЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊAЃЈ13ЃЌ0ЃЉЃЌBЃЈ11ЃЌ12ЃЉЃЌЖЏЕуPЃЌQЗжБ№ДгOЁЂBСНЕуЭЌЪБГіЗЂЃЌЕуPвдУПУы2ИіЕЅЮЛЕФЫйЖШбиOAЯђжеЕуAдЫЖЏЃЌЕуQвдУПУы1ИіЕЅЮЛЕФЫйЖШбиBCЯђCдЫЖЏЃЌЕБЕуPЭЃжЙдЫЖЏЪБЃЌЕуQЭЌЪБЭЃжЙдЫЖЏЃЎЯпЖЮOBЁЂPQЯрНЛгкЕуDЃЌЙ§ЕуDзїDEЁЮOAЃЌНЛABгкЕуEЃЌЩшЖЏЕуPЁЂQдЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКsЃЉ ШчЭМЃЌжБЯпABгыxжсИКАыжсЁЂyжсе§АыжсЗжБ№НЛгкAЁЂBСНЕуЃЌOAЁЂOBЕФГЄЖШЗжБ№ЮЊaКЭbЃЌЧвТњзуa2-2ab+b2=0ЃЌжБЯпOQгыжБЯпABНЛгкЕуQЃЌЙ§AЁЂBСНЕуЗжБ№зїAMЁЭOQгкMЃЌBNЁЭOQгкNЃЌШєAM=9ЃЌBN=4ЃЌЧѓMNЕФГЄЃЎ
ШчЭМЃЌжБЯпABгыxжсИКАыжсЁЂyжсе§АыжсЗжБ№НЛгкAЁЂBСНЕуЃЌOAЁЂOBЕФГЄЖШЗжБ№ЮЊaКЭbЃЌЧвТњзуa2-2ab+b2=0ЃЌжБЯпOQгыжБЯпABНЛгкЕуQЃЌЙ§AЁЂBСНЕуЗжБ№зїAMЁЭOQгкMЃЌBNЁЭOQгкNЃЌШєAM=9ЃЌBN=4ЃЌЧѓMNЕФГЄЃЎ