题目内容
2.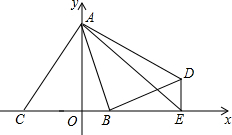 如图,点A的坐标为(0,4),点B的坐标为(1,0),点C为x轴负半轴上一点,连接AC.线段AC绕点A旋转90°至线段AD,∠BAD=45°,过点D作DE⊥x轴于E,连接BD、AE,则直线BD与直线AE的交点的横坐标为$\frac{68}{23}$.
如图,点A的坐标为(0,4),点B的坐标为(1,0),点C为x轴负半轴上一点,连接AC.线段AC绕点A旋转90°至线段AD,∠BAD=45°,过点D作DE⊥x轴于E,连接BD、AE,则直线BD与直线AE的交点的横坐标为$\frac{68}{23}$.
分析 作辅助线构造全等三角形和矩形,通过证明△AOC≌△AFD,得到AF=AO,OC=DF,由点A的坐标为(0,4),点B的坐标为(1,0),得到AF=OE=OA=EF=4,由△CAB≌△DAB,得到BC=BD,由勾股定理列方程求得点D,E的坐标,于是得到直线BD与直线AE的解析式,联立方程组求得交点的坐标.
解答 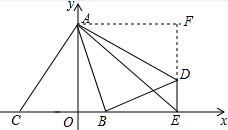 解:如图,过点A作AF⊥y轴交DE的延长线于一点F,
解:如图,过点A作AF⊥y轴交DE的延长线于一点F,
∴四边形ABEF是矩形,
∴AF=OE,OA=EF,
∵线段AC绕点A旋转90°至线段AD,
∴AD=AC,∠CAD=90°,
∴∠CA0=90°-∠OAD,
∵∠FAD=90°=∠OAD,
∴∠CAO=∠FAD,
在△CAD与△DAF中,
$\left\{\begin{array}{l}{∠AOC=∠F}\\{∠CAO=∠DAF}\\{AC=AD}\end{array}\right.$,
∴△AOC≌△AFD(AAS),
∴AF=AO,OC=DF,
∵点A的坐标为(0,4),点B的坐标为(1,0),
∴OA=4,OB=1,
∴AF=OE=OA=EF=4,
在△CAB与△DAB中,
$\left\{\begin{array}{l}{AC=AD}\\{∠CAB=DAB=45°}\\{AB=AB}\end{array}\right.$,
∴△CAB≌△DAB(SAS),
∴BC=BD,
设OC=m,则BC=BD=m+1,DE=4-m,BE=3,
∴(m+1)2=32+(4-m)2,
∴m=$\frac{12}{5}$,
∴DE=$\frac{8}{5}$,
∴E(4,0),D(4,$\frac{8}{5}$),
∴直线AE的解析式为:y=-x+4,
直线BD的解析式为:y=$\frac{8}{15}$x-$\frac{8}{15}$,
解$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{8}{15}x-\frac{8}{15}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{68}{23}}\\{y=\frac{24}{23}}\end{array}\right.$,
∴直线BD与直线AE的交点的横坐标:$\frac{68}{23}$.
故答案$\frac{68}{23}$.
点评 本题考查了全等三角形的判定与性质,图形的变换旋转,勾股定理的应用,待定系数法求函数的解析式,求直线的交点坐标,正确的作出辅助线是解题的关键.

| A. | a≤0 | B. | a≥0 | C. | a>0 | D. | a为任何实数 |
 如图,若∠C=30°,求∠A+∠B+∠D+∠E的度数.
如图,若∠C=30°,求∠A+∠B+∠D+∠E的度数.
 如图,四边形ABCD的面积为8cm2,E、F、G、H分别是四条边的中点,求四边形EFGH的面积.
如图,四边形ABCD的面积为8cm2,E、F、G、H分别是四条边的中点,求四边形EFGH的面积.
 如图,5个全等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )
如图,5个全等的正六边形,A、B、C、D、E,请仔细观察A、B、C、D四个答案,其中与右方图案完全相同的是( )


