题目内容
1.如图,在平面直角坐标系中,点A和点C分别在x轴和y轴的正半轴上,OA=6,OC=4,以OA、OC为边作矩形OABC,动点M、N分别以每秒1个单位长度的速度从点A、C同时出发,其中点M沿AO向终点O运动,点N沿CB向终点B运动,当两个动点运动了t秒,过点N作NP⊥BC,交OB于点P,连接MP.(1)直接写出点B的坐标为(6,4),直线OB的函数解析式为y=$\frac{2}{3}$x;
(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6),并求当t为何值时,S有最大值;
(3)试探究,当S有最大值时,在直线ON上是否存在点E,使△EMN为等腰三角形?若存在,求出点E的坐标;若不存在,请说明理由.

分析 (1)由OA=6,AB=4,易得点B的坐标为(6,4);由图可得,点P的横坐标=CN=t,纵坐标=4-NP,NP的值可根据相似比求得;
(2)由(1)的结论易得△OMP的高为$\frac{2}{3}$t,而OM=6-AM=6-t,再根据三角形的面积公式即可求得S与t的函数关系式,再由二次函数的最值求法,求得t为何值时,S有最大值;
(3)由(2)求得点M、N的坐标,从而求得直线ON的函数关系式;然后分两种情况考虑:①当EN=EM时,②当EN=EM时,③当ME=MN时,从而求得符合条件的点E的坐标.
解答  解:(1)延长NP交OA于H,
解:(1)延长NP交OA于H,
∵四边形OABC是矩形,
∴BC∥OA,∠OCB=90°,
∵PN⊥BC,
∴NH∥OC,
∴四边形CNHO是平行四边形,
∴OH=CN,
∵OA=6,AB=4,
∴点B的坐标为(6,4);
设直线OB的解析式为y=kx,
∴4=6k,解得k=$\frac{2}{3}$,
∴直线OB的函数解析式为y=$\frac{2}{3}$x.
故答案为(6,4)、y=$\frac{2}{3}$x.
(2)由图可得,点P的横坐标=0H=CN=t,纵坐标=4-NP,
∵NP⊥BC,
∴NP∥OC,
∴NP:OC=BN:CB,
即NP:4=(6-t):6,
∴NP=4-$\frac{2}{3}$t,
∴点P的纵坐标=4-NP=$\frac{2}{3}$t,
则点P的坐标为(t,$\frac{2}{3}$t);
∴S△OMP=$\frac{1}{2}$×OM×$\frac{2}{3}$t,
∴S=$\frac{1}{2}$×(6-t)×$\frac{2}{3}$t=-$\frac{1}{3}$t2+2t.
=-$\frac{1}{3}$(t-3)2+3(0<t<6).
∴当t=3时,S有最大值.
(3)存在.
由(2)得:当S有最大值时,点M、N的坐标分别为:M(3,0),N(3,4),
则直线ON的函数关系式为:y=$\frac{4}{3}$x.
当EN=EM时,则∠ENM=∠EMN,
∵MN⊥OA,
∴∠EOM=∠EMO,
∴OE=NE,
∴E是ON的中点,
∴E1($\frac{3}{2}$,2);
当EN=EM时,∵MN=4,OM=3
∴EN=4,ON=5,
∴OE=5-4=1或OE=5+4=9,
设E(m,$\frac{4}{3}$m),
∴OE=$\sqrt{{m}^{2}+(\frac{4}{3}m)^{2}}$=1,解得m1=$\frac{3}{5}$,m2=-$\frac{3}{5}$(舍去),
OE=$\sqrt{{m}^{2}+(\frac{4}{3}m)^{2}}$=9,解得m3=$\frac{27}{5}$,m4=-$\frac{27}{5}$(舍去),
∴E2($\frac{3}{5}$,$\frac{4}{5}$),E3($\frac{27}{5}$,$\frac{36}{5}$).
当ME=MN时,∵M(3,0),E(m,$\frac{4}{3}$m),
∴ME=$\sqrt{(m-3)^{2}+(\frac{4}{3}m)^{2}}$=4,解得m5=-$\frac{21}{25}$,m5=3(舍去),
∴E4(-$\frac{21}{25}$,-$\frac{28}{25}$),
综上所述,当S有最大值时,在直线ON上存在点E,使△EMN为等腰三角形,此时E的坐标为($\frac{3}{2}$,2)或($\frac{3}{5}$,$\frac{4}{5}$)或($\frac{27}{5}$,$\frac{36}{5}$)或(-$\frac{21}{25}$,-$\frac{28}{25}$).
点评 此题是一次函数的综合题,考查了点的坐标、待定系数法求解析式、等腰三角形的判定和性质、三角形的面积公式的应用、二次函数的最值、一次函数的应用等知识点.熟练掌握函数的特征和性质是解题的关键.

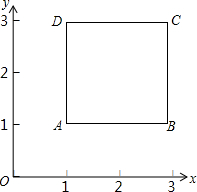 如图,正方形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,3),D(1,3).
如图,正方形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,3),D(1,3). 如图,MN是⊙O的弦,OA⊥MN于A,OA=2,以点A为圆心,OA长为半径作弧交MN于B,点B是AM的中点.
如图,MN是⊙O的弦,OA⊥MN于A,OA=2,以点A为圆心,OA长为半径作弧交MN于B,点B是AM的中点. 如图,已知直线AB、CD相交于点O,∠DOE=∠BOE,∠AOD=∠BOD+60°,求∠COE的度数.
如图,已知直线AB、CD相交于点O,∠DOE=∠BOE,∠AOD=∠BOD+60°,求∠COE的度数.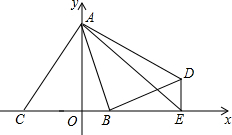 如图,点A的坐标为(0,4),点B的坐标为(1,0),点C为x轴负半轴上一点,连接AC.线段AC绕点A旋转90°至线段AD,∠BAD=45°,过点D作DE⊥x轴于E,连接BD、AE,则直线BD与直线AE的交点的横坐标为$\frac{68}{23}$.
如图,点A的坐标为(0,4),点B的坐标为(1,0),点C为x轴负半轴上一点,连接AC.线段AC绕点A旋转90°至线段AD,∠BAD=45°,过点D作DE⊥x轴于E,连接BD、AE,则直线BD与直线AE的交点的横坐标为$\frac{68}{23}$. 如图所示,直线L1的解析表达式为y=-3x+3,且L1与x轴交于点D.直线L2经过点A,B,直线L1,L2交于点C.
如图所示,直线L1的解析表达式为y=-3x+3,且L1与x轴交于点D.直线L2经过点A,B,直线L1,L2交于点C.