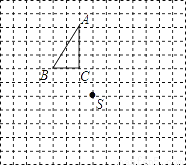��Ŀ����
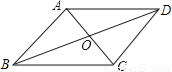
��֪����ͼ��AB��BD��CD��BD������ֱ�ΪB��D��AD��BC�ཻ�ڵ�E��EF��BD������ΪF�����ǿ���֤��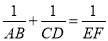 ��������Ҫ����֤������
��������Ҫ����֤������
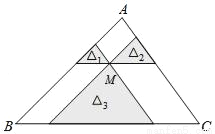
����ͼ�еĴ��߸�Ϊб������ͼ��AB��CD��AD��BC�ཻ�ڵ�E������E��EF��AB��BD�ڵ�F����
��1��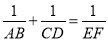 ����������������������֤�����������������˵�����ɣ�
����������������������֤�����������������˵�����ɣ�
��2�����ҳ�S��ABD��S��BED��S��BDC��Ĺ�ϵʽ��������֤����
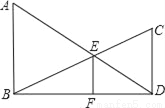
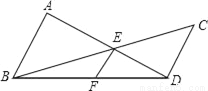
��ϰ��ϵ�д�
 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
�����Ŀ


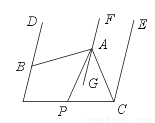
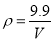 ��
�� 
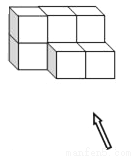
 B.
B.  C.
C.  D.
D.