题目内容
15．
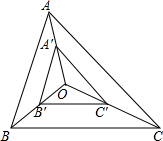如图，O为△ABC内任意一点，点A′、B′、C′分别是线段OA，OB，OC的中点，△A′B′C′与△ABC相似吗？为什么？
分析 根据三角形中位线的性质得到A′B′=$\frac{1}{2}$AB，B′C′=$\frac{1}{2}$BC，A′C′=$\frac{1}{2}$AC，于是得到$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$，即可得到结论．
解答 解：△A′B′C′与△ABC相似，
理由：∵点A′、B′、C′分别是线段OA，OB，OC的中点，
∴$\frac{A′B′}{AB}$=$\frac{1}{2}$，$\frac{B′C′}{BC}$=$\frac{1}{2}$，$\frac{A′C′}{AC}$=$\frac{1}{2}$，
∴$\frac{A′B′}{AB}$=$\frac{B′C′}{BC}$=$\frac{A′C′}{AC}$，
∴△A′B′C′∽△ABC．
点评 本题考查了相似三角形的判定：三组对应边的比相等的两个三角形相似，也考查了三角形中位线性质，熟练掌握相似三角形的判定定理是解题的关键．
练习册系列答案
相关题目
6．-$\frac{\sqrt{3}}{2}$的绝对值是（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{3}}{3}$ |
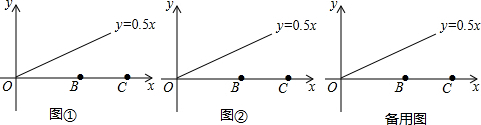
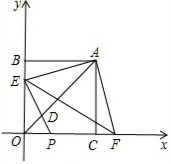在平面直角坐标系中，点A（m，m）在第一象限，且实数m满足条件：|$\sqrt{3}$-m|=m-$\sqrt{m-4}$，AB⊥y轴于B，AC⊥x轴于C