题目内容
 如图,已知直线y=
如图,已知直线y=| 3 |
| 4 |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:探究型
分析:将y=
x+3和y=
组成方程组,分别建立关于x和y的一元二次方程,求出C、D的水平距离和垂直距离表达式,利用勾股定理建立关于k的方程,解答即可.
| 3 |
| 4 |
| k |
| x |
解答:解:将y=
x+3和y=
组成方程组得,
,
整理得,
x+3=
,
即3x2+12x-4k=0,
则C、D的水平距离为|x1-x2|=
=
=
;
将y=
x+3和y=
组成方程组得,
,
整理得4y2=3k+12y,
即4y2-12y-3k=0,
则C、D的垂直距离为|y1-y2|=
=
=
;
由勾股定理得,16+
k+9+3k=32;
解得,k=-
.
故答案为-
.
| 3 |
| 4 |
| k |
| x |
|
整理得,
| 3 |
| 4 |
| k |
| x |
即3x2+12x-4k=0,
则C、D的水平距离为|x1-x2|=
| (x1+x2)2-4x1x2 |
(-4)2-4(-
|
16+
|
将y=
| 3 |
| 4 |
| k |
| x |
|
整理得4y2=3k+12y,
即4y2-12y-3k=0,
则C、D的垂直距离为|y1-y2|=
| (y1+y2)2-4y1y2 |
32-4(-
|
| 9+3k |
由勾股定理得,16+
| 16 |
| 3 |
解得,k=-
| 48 |
| 25 |
故答案为-
| 48 |
| 25 |
点评:本题考查了反比例函数与一次函数的交点问题,将此题转化为水平距离和垂直距离是解答的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
一个圆锥的侧面积是底面积的3倍,则这个圆锥的侧面展开图的圆心角的度数为( )
| A、180° | B、120° |
| C、90° | D、60° |
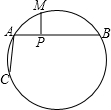 已知M是弧CAB的中点,MP垂直弦AB于P,若弦AC的长度为x,线段AP的长度是x+1,那么线段PB的长度是( )
已知M是弧CAB的中点,MP垂直弦AB于P,若弦AC的长度为x,线段AP的长度是x+1,那么线段PB的长度是( )| A、2x+1 | B、2x+2 |
| C、2x+3 | D、3x+1 |
 如图所示,图的主视图是( )
如图所示,图的主视图是( )A、 |
B、 |
C、 |
D、 |
若AM是△ABC的中线,
=2
,
=2
,则
=( )
| AB |
| a |
| AC |
| b |
| AM |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图是反比例函数
如图是反比例函数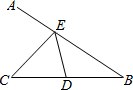 如图,∠ABC=30°,BC=4,D是BC边的中点,E是边BA上一动点,则EC+ED的最小值是
如图,∠ABC=30°,BC=4,D是BC边的中点,E是边BA上一动点,则EC+ED的最小值是