题目内容
7．
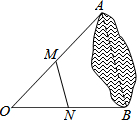如图，为估计池塘两岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA、OB的中点M，N，测得MN=39m，则A，B两点间的距离是78m．
分析 根据M、N是OA、OB的中点，即MN是△OAB的中位线，根据三角形的中位线定理：三角形的中位线平行于第三边且等于第三边的一半，即可求解．
解答 解：∵M、N是OA、OB的中点，即MN是△OAB的中位线，
∴MN=$\frac{1}{2}$AB，
∴AB=2MN=2×39=78（m）．
故答案为78．
点评 本题考查了三角形的中位线定理应用，学会利用三角形中位线定理求池塘的宽是解题的关键．
练习册系列答案
相关题目
14．下列四个几何体中，已知某个几何体的主视图、左视图、俯视图分别为圆、长方形、长方形，则该几何体是（ ）
| A． | 圆锥体 | B． | 圆柱体 | C． | 球体 | D． | 长方体 |
18．某学校初、高中六个年级共有3000名学生，为了解其视力情况，现采用抽样调查，各年级人数如下表所示：
（1）如果按10%的比例抽样，样本是什么？样本容量是多少？
（2）考虑到不同年级学生的视力差异，为了保证样本有较好的代表性，各年级分别应调查多少人？将结果填写在上面的表中；
（3）如果要从你所在的班50名学生中抽取5人进行调查，请设计一个抽样方案，保证每人有相同的机会被抽到．
| 年级 | 七年级 | 八年级 | 九年级 | 高一 | 高二 | 高三 | 合计 |
| 人数/名 | 560 | 520 | 500 | 500 | 480 | 440 | 3000 |
| 调查数/名 | 56 | 52 | 50 | 50 | 48 | 44 | 300 |
（2）考虑到不同年级学生的视力差异，为了保证样本有较好的代表性，各年级分别应调查多少人？将结果填写在上面的表中；
（3）如果要从你所在的班50名学生中抽取5人进行调查，请设计一个抽样方案，保证每人有相同的机会被抽到．
