Question

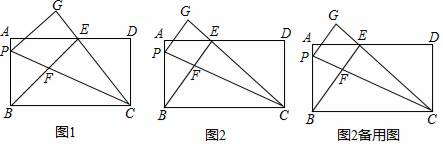
【题目】 有一款如图（1）所示的健身器材，可通过调节AB的长度来调节椅子的高度，其平面示意图如图（2）所示，经测量，AD与DE的夹角为75°，AC与AD的夹角为45°，且DE∥AB．现调整AB的长度，当∠BCA为75°时测得点C到地面的距离为25cm．请求出此时AB的长度（结果保留根号）．

Answer 1

【答案】AB的长度是cm．

【解析】

作CG⊥AD于点G，作CF⊥AB于点F，通过解直角三角形求得AF，BF的长度，本题得以解决．

解：

由已知可得，

∠EDA=75°，∠BCA=75°，∠CAG=45°，CG=25cm，

∴AC= ，

∵DE∥AB，

∴∠EDA+∠BAD=180°，

∴∠BAD=105°，

∴∠CAF=60°，

∵∠CFA=90°，AC=25，

∴∠ACF=30°，

∴AF=，CF=，

∵∠ACB=75°，∠ACF=30°，∠CFB=90°，CF=，

∴∠BCF=45°，

∴BF=CF=，

∴AB=AF+BF==cm，

答：此时AB的长度是cm．