题目内容
6.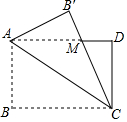 如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )
如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )| A. | AM=AB | B. | ∠ACB′=∠DCM | C. | ∠BAC=∠CMD | D. | AM=MC |
分析 轨迹翻转变换的性质得到AB′=AB=CD,∠B′=∠B=90°,证明△AB′M≌△CDM,根据全等三角形的性质解答即可.
解答 解:由折叠的性质可知,AB′=AB=CD,∠B′=∠B=90°,
在△AB′M和△CDM中,
$\left\{\begin{array}{l}{∠B′=∠D}\\{∠AMB′=∠CMD}\\{AB′=CD}\end{array}\right.$,
∴△AB′M≌△CDM,
∴AM=MC,
故选:D.
点评 本题考查的是翻转变换的性质、矩形的性质,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
16.已知点A的坐标为(2,3),O为坐标原点,连接OA,将线段OA绕点A按顺时针方向旋转90°得AB,则点B的坐标为( )
| A. | (5,1) | B. | (-3,2) | C. | (-1,5) | D. | (3,-2) |
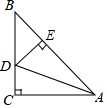 在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=7 cm,则AC+CD的长等于7.
在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E.若AB=7 cm,则AC+CD的长等于7.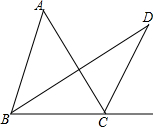 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°.
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°. 实数a、b在数轴上的对应位置如图所示,化简|-b|+|a|的结果为b-a.
实数a、b在数轴上的对应位置如图所示,化简|-b|+|a|的结果为b-a.