题目内容
14.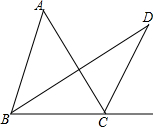 如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°.
如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=40°,则∠D的度数是20°.
分析 根据角平分线的定义得到∠DCE=$\frac{1}{2}$∠ACE,∠DBC=$\frac{1}{2}$∠ABC,根据三角形的外角的性质计算即可.
解答 解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,
∴∠DCE=$\frac{1}{2}$∠ACE,∠DBC=$\frac{1}{2}$∠ABC,
又∠D=∠DCE-∠DBC,∠A=∠ACE-∠ABC,
∴∠D=$\frac{1}{2}$∠A=20°.
故答案为:20°.
点评 本题考查的是三角形的外角的性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列各式中,单项式为( )
| A. | x+1 | B. | $\frac{{{x}^{2}y}^{2}}{4}$ | C. | $\frac{1}{x}$ | D. | 4y2-5 |
19. 如图,∠1=25°,则射线OA表示为( )
如图,∠1=25°,则射线OA表示为( )
 如图,∠1=25°,则射线OA表示为( )
如图,∠1=25°,则射线OA表示为( )| A. | 南偏西65° | B. | 南偏西25° | C. | 南偏东65° | D. | 南偏东25°. |
6.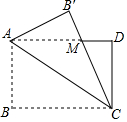 如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )
如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )
 如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )
如图,将矩形ABCD的△ABC以AC为轴对折得△AB′C,使B′C与AD交于点M,则下列结论正确的是( )| A. | AM=AB | B. | ∠ACB′=∠DCM | C. | ∠BAC=∠CMD | D. | AM=MC |
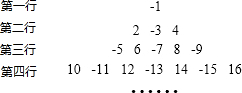 将有理数-1,2,-3,4,-5,6,-7,…排成如图的形式(下一行比上一行多两个数),观察各行右边的数的规律,按此规律推算第10行从左边数第4个数是-85.
将有理数-1,2,-3,4,-5,6,-7,…排成如图的形式(下一行比上一行多两个数),观察各行右边的数的规律,按此规律推算第10行从左边数第4个数是-85. 如图,将两块直角三角尺的直角顶点O叠放在一起,若∠AOD=130°,则∠BOC的度数为50°.
如图,将两块直角三角尺的直角顶点O叠放在一起,若∠AOD=130°,则∠BOC的度数为50°.