题目内容
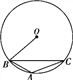
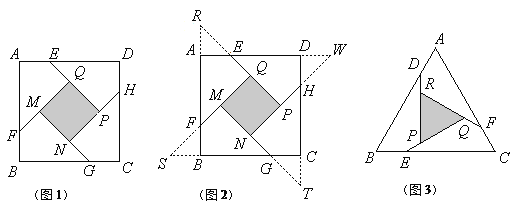
【题目】元旦那天,6位朋友均匀地围坐在圆桌旁共度佳节.如图,圆桌半径为60 cm,每人离圆桌的距离均为10 cm,现又来了两名客人,每人向后挪动了相同的距离,再左右调整位置,使8人都坐下,并且8人之间的距离与原来6人之间的距离(即在圆周上两人之间的圆弧的长)相等.设每人向后挪动的距离为x,根据题意,可列方程( ).
A. ![]() =
=![]()
B. ![]()
C. 2π(60+10)×6=2π(60+π)×8
D. 2π(60-x)×8=2π(60+x)×6
【答案】A
【解析】
本题考查的是由实际问题抽象出一元一次方程。首先理解题意找出题中存在的等量关系:坐6个人时两人之间的距离=坐8个人时两人之间的距离,根据等量关系列方程即可。解:设每人向后挪动的距离为xcm,应首先明确弧长公式:![]() ,
,
六位朋友每相邻两人之间的弧长所对的圆心角度数为60°,半径为(60+10)cm,
即![]()
八位朋友每相邻两人之间的弧长所对的圆心角度数为45°,半径为60+10+x,
即![]()
根据距离相等可列方程为![]() ,故选A
,故选A

练习册系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
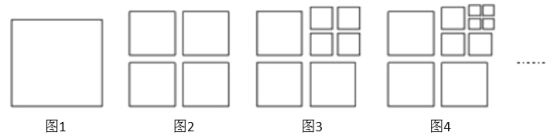
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?