Question

【题目】小烨在探究数轴上两点间距离时发现：若两点在轴上或与轴平行，两点的横坐标分别为，则两点间距离为；若两点在轴上或与轴平行，两点的纵坐标分别为，则两点间距离为.据此，小烨猜想：对于平面内任意两点，两点间的距离为.

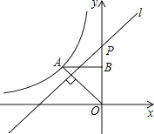
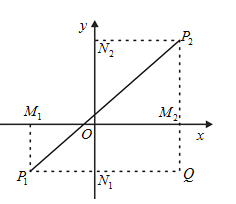
（1）请你利用下图，试证明：；

（2）若，试在轴上求一点，使的距离最短，并求出的最小值和点坐标．

Answer 1

【答案】（1） （2）点坐标为

【解析】分析：（1）直接利用两点之间距离公式直接证明即可；

（2）利用轴对称求最短路线方法得出M点位置，进而求出|MA|+|MB|的最小值.

（1）证明：如图所示，

从、分别向轴和轴作垂线

和 ，垂足分别为、

、、，

其中直线和相交于点．

在中，

∵ ,

．

∴ ．

∴

（2）作点关于轴的对称点，连接，与两点间的距离即为所求的最小值，直线与轴的交点为所求的点

∴＝

设直线的解析式为，则依题意得

解得：

∴直线的解析式为，

令得：

∴ 的最小值为5，点坐标为.