题目内容
在数学中,为了书写简便,18世纪数学家欧拉就引进了求和符号“∑ ”.如记
k=1+2+3+…+(n-1)+n,
(x+k)=(x+3)+(x+4)+…+(x+n);已知
[(x+k)(x-k+1)]=4x2+4x+m,则m的值是( )
| n |
 |
| k=1 |
| n |
 |
| k=3 |
| n |
 |
| k=2 |
| A、40 | B、-70 |
| C、-40 | D、-20 |
考点:平方差公式
专题:新定义
分析:由x2项的系数可知n=5,然后列出算式进行计算,再根据常数项相等解答.
解答:解:∵x2项的系数是4,
∴n=5,
∴(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)
=(x2+x-2)+(x2+x-6)+(x2+x-12)+(x2+x-20)
=4x2+4x-40,
∵
[(x+k)(x-k+1)]=4x2+4x+m,
∴m=-40.
故选C.
∴n=5,
∴(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)
=(x2+x-2)+(x2+x-6)+(x2+x-12)+(x2+x-20)
=4x2+4x-40,
∵
| n |
 |
| k=2 |
∴m=-40.
故选C.
点评:本题考查了平方差公式,读懂题目信息,理解求和符号的定义并判断出n=5是解题的关键.

练习册系列答案
相关题目
若|x+3|+
=0,则x+y的值为( )
| y-2 |
| A、1 | B、-1 | C、5 | D、-5 |
下列代数式的意义表述不正确的是( )
| A、a+2b的意义是a与2b的和 | ||||
B、x-
| ||||
| C、m(n+3)的意义是m乘以(n+3) | ||||
| D、(a+b)2的意义是a加上b的平方 |
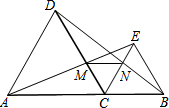 如图,点C为线段AB上一动点(不与点A,B重合),在AB同侧分别作等边△ACD和等边△CBE,连结AE与BD,AE与CD交于点M,CE与BD交于点N,连结MN,则对于结论①AE=DB;②EM=BN;③△CMN是等边三角形;④MN∥AB,其中正确结论的个数是( )
如图,点C为线段AB上一动点(不与点A,B重合),在AB同侧分别作等边△ACD和等边△CBE,连结AE与BD,AE与CD交于点M,CE与BD交于点N,连结MN,则对于结论①AE=DB;②EM=BN;③△CMN是等边三角形;④MN∥AB,其中正确结论的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
若长方形的周长为16,其邻边a、b为整数,且满足a2+b2+3ab=76,则长方形的面积为( )
| A、6 | B、8 | C、10 | D、12 |
若2是方程x2+4x+c=0的一个根,则c的值是( )
| A、6 | B、-8 | C、-10 | D、-12 |
若直角三角形斜边上的高和中线分别是5cm,8cm,则这个三角形的面积是( )
| A、80cm2 |
| B、60cm2 |
| C、40cm2 |
| D、20cm2 |
 如图,BC⊥AB,则图中四边形OABC的面积为
如图,BC⊥AB,则图中四边形OABC的面积为 探究:如图,长方形ABCD的长为4,宽为2.
探究:如图,长方形ABCD的长为4,宽为2.